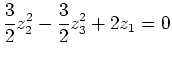Bestimmen Sie für die Quadrik
die Normalform.
Geben Sie für jeden Transformationsschritt und
für die Gesamttransformation jeweils das neu gewählte Koordinatensystem und
die Koordinatentransformation an. Skizzieren Sie die Quadrik.
Zunächst stellen wir die Gleichung der Quadrik in Matrizenform auf und setzen
dazu
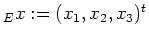 :
:
Nun drehen wir als nächstes das Koordinatensystem, d.h. wir führen eine
Hauptachsentransformation durch. Die Eigenwerte der Matrix sind 0, 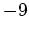 und
und
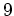 . Die Matrix der zugehörigen Eigenvektoren hat folgende Gestalt:
. Die Matrix der zugehörigen Eigenvektoren hat folgende Gestalt:
Wir transformieren auf das neue Koordinatensystem
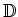 , das von diesen
Eigenvektoren aufgespannt wird durch
, das von diesen
Eigenvektoren aufgespannt wird durch
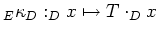 . Die Quadrik
. Die Quadrik 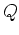 hat in den neuen
Koordinaten dann folgende Gleichung (einsetzen von
hat in den neuen
Koordinaten dann folgende Gleichung (einsetzen von
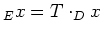 ):
):
Mittels quadratischem Ergänzen errechnen wir die nächste
Koordinatentransformation
Damit erhalten wir die Quadrik in der Gleichung (mit
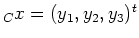 ):
):
Zuletzt verschieben wir noch, um den konstanten Term zu eliminieren mittels
Damit erhalten wir als euklidische Normalform der Quadrik 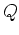 (mit
(mit
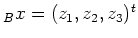 ):
):
Damit erweist sich 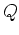 als hyperbolisches Paraboloid.
als hyperbolisches Paraboloid.
(Ackermann/Poppitz)
| |
automatisch erstellt
am 17. 2. 2006 |


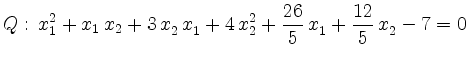
![]() :
:
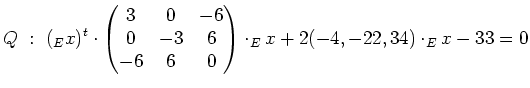
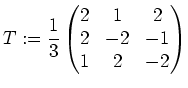
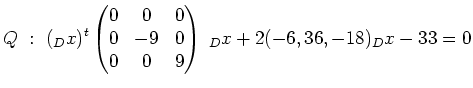
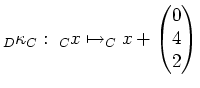
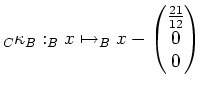
![]() (mit
(mit
![]() ):
):