Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Interaktive Aufgabe 990: Untersuchen mehrerer Folgen auf Monotonie und Beschränktheit

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
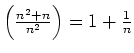  1. Es ist $ \left(\frac{n^2+n}{n^2}\right)=1+\frac{1}{n}$. Die Folge ist streng monoton fallend, denn $ 1+\frac1n>1+\frac{1}{n+1}$. Ausserdem sind alle Folgenglieder größer als $ 1$, was also eine untere Schranke darstellt. Da die Folge streng monoton fallend ist muss sie auch nach oben beschränkt sein, nämlich durch ihr erstes Glied, sie ist also nach oben durch $ 2$ beschränkt.
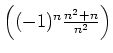  2. Die Folge $ \left( (-1)^n\frac{n^2+n}{n^2}\right)$ ist sicher nicht monoton, da die Glieder abwechselnd negativ und positiv sind. Der Betrag der Folge ist allerdings der selbe wie bei (a), der Betrag ist also nach oben und unten beschränkt. Aber dann ist auch die Folge selbst beschränkt mit Schranken $ \pm 2$.
  3. Die Folge $ (2n+\sin(n))$ ist streng monoton steigend denn $ 2(n+1)+\sin(n+1)-2n-\sin(n)=2+\sin(n+1)-\sin(n)$. Die Differenz $ \sin(n)-\sin(n+1)$ kann höchstens $ 2$ betragen, denn der Sinus nimmt nur Werte zwischen $ -1$ und $ +1$ an. Aber diese Maximaldifferenz kommt nur vor, wenn der Abstand genau $ \pi$ beträgt. Daher ist $ \vert\sin(n+1)-\sin(n)\vert<2$ und die Folge damit streng monoton steigend.

    Die Folge ist damit natürlich nach unten durch $ 0<2+\sin(1)$ beschränkt. Nach oben ist sie unbeschränkt denn wir können abschätzen:

    $\displaystyle \vert 2n+\sin(n)\vert\geq \vert 2n\vert-\vert\sin(n)\vert\geq 2n-1$    

    Letzteres strebt gegen $ +\infty$ für $ n\to\infty$.
  4. Die Folge $ (2\pi n+n\sin(n))$ ist weder beschränkt noch monoton. Das Letztere sieht man auf folgende Weise:

    $\displaystyle (2\pi(n+1)+(n+1)\sin(n+1))-(2\pi n +n\sin(n))=2\pi+sin(n+1)+n(\sin(n+1)-\sin(n))$    

    Der letzte Term darin kann mit $ n$ beliebig gross werden und wegen der Differenz der Sinusfunktionen sowohl positiv als auch negativ. Daher ist die Folge nicht monoton.

    Die Folge ist auch nicht beschränkt, denn wie in (3) schätzen wir ab

    $\displaystyle \vert 2\pi n+n\sin(n)\vert\geq n(\vert 2\pi\vert - \vert\sin(n)\vert)\geq n(2\pi -1).$    

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 17.  2. 2006