Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 1283: Vektorraum der Treppenfunktionen

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 1283: Vektorraum der Treppenfunktionen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Zeigen Sie, dass

die Treppenfunktionen auf dem Intervall einen $\R$ -Vektorraum bilden,
die punktweise Multiplikation zweier Treppenfunktionen auf dem Intervall wieder eine Treppenfunktion bezüglich der Zerlegung $Z_{fg}=Z_f\cup Z_g$ ist,
die Treppenfunktionen auf dem Intervall mit obiger Multiplikation einen Ring bilden.

i) Dass die Menge der Treppenfunktionen nicht leer ist, ist klar, da alle über

konstanten Funktionen Treppenfunktionen sind. Die Menge aller Funktionen $[a,b] \, \to\nobreakspace\, \mathbb{R}$ bildet einen $\mathbb{R}$ -Vektorraum. Für die Menge der Treppenfunktionen kann das Untervektorraum-Kriterium angewendet werden. Wir definieren zuerst die charakteristische Funktion einer Menge $M\subseteq [a,b]$ als

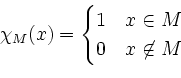
$\begin{displaymath} \chi_{M}(x)= \begin{cases} 1 & x\in M\\ 0 & x\not\in M \end{cases}\end{displaymath}$

homogen
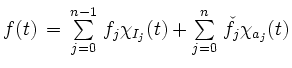Sei $\lambda \in \mathbb{R}$ und $f(t) \, = \, \sum\limits_{j=0}^{n-1} \, f_{j} \chi_{I_{j}}(t) + \sum\limits_{j=0}^{n} \, \check{f}_{j}\chi_{a_j}(t)$ eine Treppenfunktion mit Intervallen $I_{j}=(a_j,a_j+1)$ , die disjunkt überdecken.
Dann ist auch 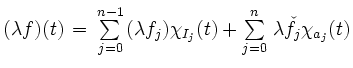$(\lambda f)(t) \, = \, \sum\limits_{j=0}^{n-1} \, (\lambda f_{j}) \chi_{I_{j}}(t)+ \sum\limits_{j=0}^{n} \, \lambda\check{f}_{j}\chi_{a_j}(t)$ eine Treppenfunktion.
additiv
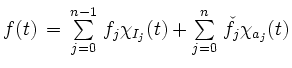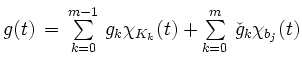Seien $f(t) \, = \, \sum\limits_{j=0}^{n-1} \, f_{j} \chi_{I_{j}}(t) + \sum\limits_{j=0}^{n} \, \check{f}_{j}\chi_{a_j}(t)$ und $g(t) \, = \, \sum\limits_{k=0}^{m-1} \, g_{k} \chi_{K_{k}}(t)+\sum\limits_{k=0}^{m} \, \check{g}_{k} \chi_{b_j}(t)$ Treppenfunktionen. Dabei seien jeweils $I_{j} = (a_{j},a_{j+1})$ und $K_{k} = (b_{k},b_{k+1})$ . $(c_{0},\ldots,c_{n+m+1})$ seien die Elemente der Menge $\{a_{0},\ldots,a_{n},b_{0},\ldots,b_{m}\}$ in aufsteigender Anordnung. Sowohl als auch können also als Treppenfunktionen

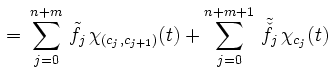$\displaystyle f(t)$ $\displaystyle \, = \, \sum\limits_{j=0}^{n+m} \, \tilde{f}_{j} \, \chi_{(c_{j},c_{j+1})}(t)+ \sum\limits_{j=0}^{n+m+1} \, \tilde{\check{f}}_{j} \, \chi_{c_j}(t)$

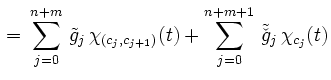$\displaystyle g(t)$ $\displaystyle \, = \, \sum\limits_{j=0}^{n+m} \, \tilde{g}_{j} \, \chi_{(c_{j},c_{j+1})}(t)+ \sum\limits_{j=0}^{n+m+1} \, \tilde{\check{g}}_{j} \, \chi_{c_j}(t)$

mit gemeinsamer Intervallunterteilung dargestellt werden. Als Summe ergibt sich

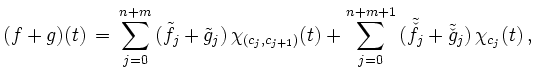$\displaystyle (f+g)(t) \, = \, \sum\limits_{j=0}^{n+m} \, (\tilde{f}_{j} + \til... ...^{n+m+1} \, (\tilde{\check{f}}_{j} + \tilde{\check{g}}_{j}) \, \chi_{c_j}(t)\,,$

wiederum also eine Treppenfunktion.

Damit ist gezeigt, dass die Menge der Treppenfunktionen ein $\mathbb{R}$ -Vektorraum ist.

ii) Seien und zwei Treppenfunktionen. Wie in Teil i) kann man auch hier eine gemeinsame Intervallunterteilung finden, so dass

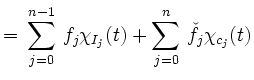$\displaystyle f(t)$	$\displaystyle = \, \sum\limits_{j=0}^{n-1} \, f_{j} \chi_{I_{j}}(t)+ \sum\limits_{j=0}^{n} \, \check{f}_{j}\chi_{c_j}(t)$
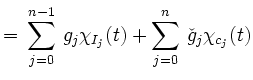$\displaystyle g(t)$	$\displaystyle = \, \sum\limits_{j=0}^{n-1} \, g_{j} \chi_{I_{j}}(t)+ \sum\limits_{j=0}^{n} \, \check{g}_{j}\chi_{c_j}(t)$

gilt. Da die Multiplikation punktweise definiert wird, gilt

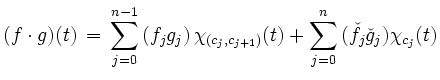$\displaystyle (f\cdot g)(t) \, = \, \sum\limits_{j=0}^{n-1} \, (f_{j} g_{j}) \,... ...j+1})}(t) + \sum\limits_{j=0}^{n} \, (\check{f}_{j} \check{g}_{j})\chi_{c_j}(t)$

und die entstandene Funktion ist wieder eine Treppenfunktion.

iii) Aus i) folgt, dass die Treppenfunktionen bezüglich der Addition eine Abelsche Gruppe bilden. Zu untersuchen ist noch, dass es sich bzgl. der Multiplikation um eine Halbgruppe handelt und die Distributivgesetze gelten. Abgeschlossenheit bzgl. der Multiplikation wurde in ii) gezeigt. Die Kommutativ-, Assoziativ- und Distributivgesetze vererben sich aus den entsprechenden Gesetzen in $\mathbb{R}$ , da Addition und Multiplikation jeweils punktweise definiert sind. Als -Element tritt die Treppenfunktion $f \equiv 1$ auf.

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)

[Zurück zur Aufgabe]

automatisch erstellt am 20. 6. 2006

$\displaystyle f(t)$	$\displaystyle \, = \, \sum\limits_{j=0}^{n+m} \, \tilde{f}_{j} \, \chi_{(c_{j},c_{j+1})}(t)+ \sum\limits_{j=0}^{n+m+1} \, \tilde{\check{f}}_{j} \, \chi_{c_j}(t)$
$\displaystyle g(t)$	$\displaystyle \, = \, \sum\limits_{j=0}^{n+m} \, \tilde{g}_{j} \, \chi_{(c_{j},c_{j+1})}(t)+ \sum\limits_{j=0}^{n+m+1} \, \tilde{\check{g}}_{j} \, \chi_{c_j}(t)$