Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1306: Matrizen und lineare Gleichungssysteme

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Es seien

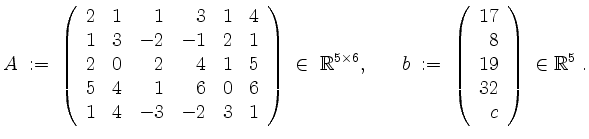
$\displaystyle A \; :=\; \left(\begin{array}{rrrrrr} 2& 1& 1& 3& 1& 4\\ 1& 3& -... ...egin{array}{rrrrr} 17\\ 8\\ 19\\ 32\\ c\end{array}\right)\;\in\mathbb{R}^5\; . $

Für welche $ c\in\mathbb{R}$ ist das Gleichungssystem $ Ax=b$ lösbar?

Bestimme die Lösungsmenge des Gleichungssystems $ Ax=b$ für solche Parameter $ c$ .

Wir bringen die erweiterte Koeffizientenmatrix $ (A\vert b)$ auf Zeilenstufenform.

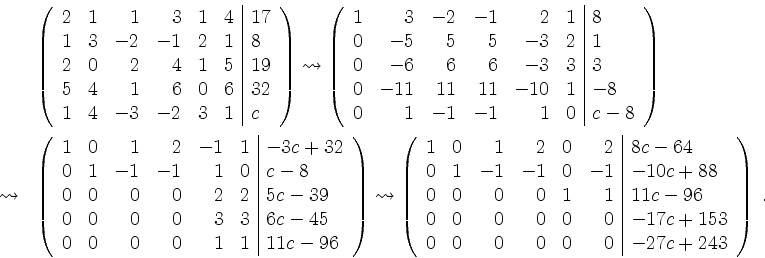
\begin{displaymath} \begin{array}{rl} &\left(\begin{array}{rrrrrr\vert l} 2& 1&... ... 0& 0& 0& 0& 0& -27c+243\\ \end{array}\right) \; . \end{array}\end{displaymath}

Also ist das Gleichungssystem lösbar genau dann, wenn $ -27c+243=0$ und $ -17c+153=0$ sind. Diese beiden Bedingungen sind aber gleichbedeutend mit $ c=9$ .

D.h. für $ c\neq 9$ ist das Gleichungssystem unlösbar, und wir erhalten die leere Lösungsmenge $ L(A,b) = \emptyset$ .

Um die Lösungsmenge für $ c=9$ zu bestimmen, setzen wir dies ein und rechnen weiter. Nullzeilen müssen nicht mitgeführt werden.

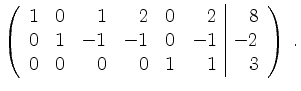
$\displaystyle \left(\begin{array}{rrrrrr\vert r} 1& 0& 1& 2& 0& 2& 8\\ 0& 1& -1& -1& 0& -1& -2\\ 0& 0& 0& 0& 1& 1& 3\\ \end{array}\right) \; . $

Die ausgewählten Spalten sind $ 1$ , $ 2$ und $ 5$ . Die nicht ausgewählten Spalten sind $ 3$ , $ 4$ und $ 6$ .

Positives Einfüllen gibt eine partikuläre Lösung

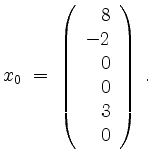
$\displaystyle x_0 \; =\; \left(\begin{array}{r}8\\ -2\\ 0\\ 0\\ 3\\ 0\end{array}\right)\;. $

Negatives Einfüllen gibt Lösungen des zugehörigen homogenen Gleichungssystems

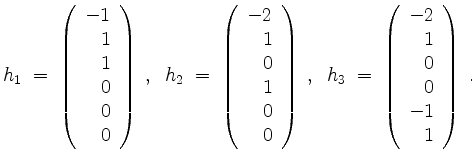
$\displaystyle h_1 \; =\; \left(\begin{array}{r} -1\\ 1\\ 1\\ 0\\ 0\\ 0\end{arra... ..._3 \; =\; \left(\begin{array}{r} -2\\ 1\\ 0\\ 0\\ -1\\ 1\end{array}\right)\; . $

Die Lösungsmenge ist also

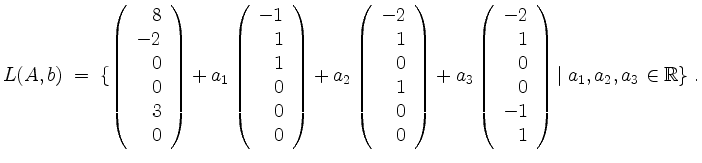
$\displaystyle L(A,b) \;=\; \{\left(\begin{array}{r}8\\ -2\\ 0\\ 0\\ 3\\ 0\end{... ...\\ 1\\ 0\\ 0\\ -1\\ 1\end{array}\right)\vert\; a_1,a_2,a_3\in\mathbb{R}\} \; . $

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006