Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1307: Basen von Vektorrämen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Sei $ V$ ein Vektorraum über dem Körper $ \mathbb{R}$ mit einer Basis $ (x_1,x_2,x_3,x_4)$ . Sei

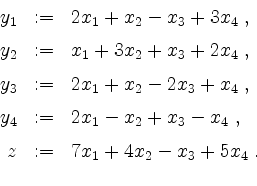
\begin{displaymath} \begin{array}{rcl} y_1 &:=& 2x_1 + x_2 -x_3 + 3x_4\;,\vspace... ... z &:=& 7x_1 + 4x_2 -x_3 +5x_4\; .\vspace*{2mm}\\ \end{array}\end{displaymath}

  1. Zeige, daß $ (y_1,y_2,y_3,y_4)$ eine Basis von $ V$ ist.
  2. Sei $ U_1:=\langle y_1,y_2,y_3\rangle$ , und sei $ U_2:=\langle y_4,z\rangle$ .
    Bestimme Basen von $ U_1\cap U_2$ und $ U_1+U_2$ .

  1. Wir zeigen, daß $ (y_1,y_2,y_3,y_4)$ linear unabhängig ist. Seien dazu $ \lambda_1,\lambda_2,\lambda_3,\lambda_4\in K$ so, daß $ \lambda_1 y_1+\lambda_2 y_2+ \lambda_3 y_3+ \lambda_4 y_4=0$ . Es wird

    \begin{displaymath} \begin{array}{rcl} 0 &=& \lambda_1(2x_1 + x_2 -x_3 + 3x_4)+... ... (3\lambda_1+2\lambda_2+\lambda_3-\lambda_4) x_4\;. \end{array}\end{displaymath}

    Wegen der linearen Unabhngigkeit des Tupels $ (x_1,x_2,x_3,x_4)$ folgt daraus das lineare Gleichungssystem

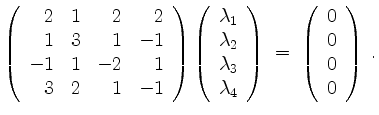
    $\displaystyle \left(\begin{array}{rrrr} 2& 1& 2& 2\\ 1& 3& 1& -1\\ -1& 1& -2&... ...d{array}\right) \;=\; \left(\begin{array}{r}0\\ 0\\ 0\\ 0\end{array}\right)\;. $

    Diese Matrix bringen wir in Zeilenstufenform. Hierbei verwenden wir, daß alle Zeilenumformungen zugelassen sind, nicht nur die im Standardalgorithmus auftretenden.

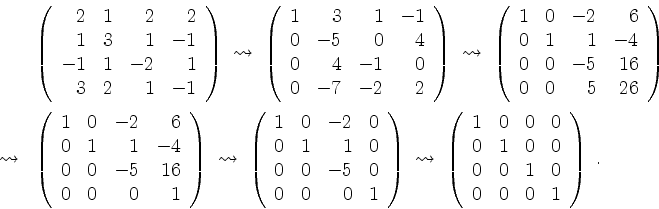
    \begin{displaymath} \begin{array}{rl} & \left(\begin{array}{rrrr} 2& 1& 2& 2\\ ... ... 1& 0\\ 0& 0& 0& 1 \\ \end{array}\right)\; . \\ \end{array}\end{displaymath}

    Daran sieht man, daß wir nur die triviale Lösung für 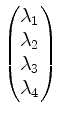$ \begin{pmatrix}\lambda_1\\ \lambda_2\\ \lambda_3\\ \lambda_4\end{pmatrix}$ haben.

    Insbesondere ist das Tupel $ (y_1,y_2,y_3.y_4)$ linear unabhängig, und wegen $ \dim V=4$ also eine Basis von $ V$ .

  2. Abweichend vom Zassenhaus-Algorithmus kann man auch wie folgt argumentieren.

    Es gilt

    $\displaystyle U_1+U_2 \;=\; \langle y_1,y_2,y_3,y_4,z\rangle \;=\; V\;, $

    weil bereits $ (y_1,y_2,y_3,y_4)$ eine Basis von $ V$ ist. Also ist $ \dim(U_1+U_2)=4$ , und $ (y_1,y_2,y_3,y_4)$ ist auch eine Basis von $ U_1+U_2$ .

    Ferner ist $ (y_4,z)$ linear unabhängig, d.h. $ \dim(U_2)=2$ . Nach der Dimensionsformel wird

    $\displaystyle \dim (U_1\cap U_2) \;=\; \dim U_1 + \dim U_2 - \dim(U_1+U_2) \;=\; 3+2-4 \;=\; 1\;. $

    Wegen $ z=y_1+y_2+y_3+y_4$ ist

    $\displaystyle y_1+y_2+y_3 \;=\; z-y_4 \;\in\; U_1\cap U_2\;. $

    Da $ y_1+y_2+y_3 = 5x_1+5x_2-2x_3+6x_4\ne 0$ , bildet also $ (5x_1+5x_2-2x_3+6x_4)$ eine Basis von $ U_1\cap U_2$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006