Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 1308: Eine Aufgabe zur direkten Summe von Polynomrämen

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 1308: Eine Aufgabe zur direkten Summe von Polynomrämen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei $V=\mathbb{C}[X]$ . Für $0\leq k\leq 3$ sei

$\displaystyle U_k \; := \; \{p\in\mathbb{R}[X]\vert\, p(\mathrm{i}X)= \mathrm{i}^k p(X)\}\; .$

Zeige, daß

$\displaystyle V \;=\; U_0\oplus U_1\oplus U_2\oplus U_3 \; .$

Wir müssen zeigen, daß

, und daß aus

$\displaystyle q_0(X) + q_1(X) + q_2(X)+ q_3(X) \; =\; 0$

mit $q_k(X)\in U_k$ folgt, daß alle

sind.

Sei zunächst $p\in V$ . Mit

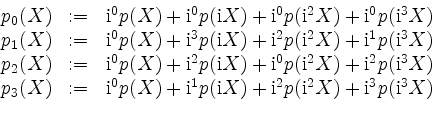
$\begin{displaymath} \begin{array}{rcl} p_0(X) &:=& \mathrm{i}^0 p(X) + \mathrm{i... ...\mathrm{i}^2 X) + \mathrm{i}^3 p(\mathrm{i}^3 X)\\ \end{array}\end{displaymath}$

ist

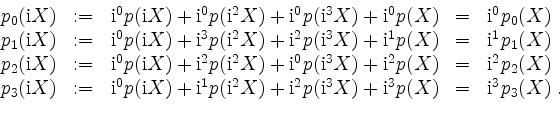
$\begin{displaymath} \begin{array}{rclcl} p_0(\mathrm{i}X) &:=& \mathrm{i}^0 p(\m... ... \mathrm{i}^3 p(X) & = & \mathrm{i}^3 p_3(X)\; .\\ \end{array}\end{displaymath}$

Somit liegt $p_k(X)\in U_k$ für alle $k\in\{0,1,2,3\}$ , so daß

zeigt, daß

Sei nun

$\displaystyle q_0(X) + q_1(X) + q_2(X)+ q_3(X) \; =\; 0$

mit $q_k(X)\in U_k$ . Es folgt

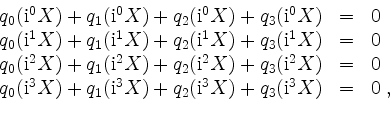
$\begin{displaymath} \begin{array}{rcl} q_0(\mathrm{i}^0 X) + q_1(\mathrm{i}^0 X)... ...mathrm{i}^3 X)+ q_3(\mathrm{i}^3 X) & = & 0\; , \\ \end{array}\end{displaymath}$

d.h.

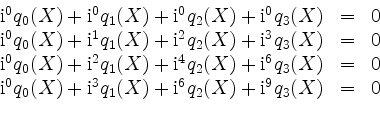
$\begin{displaymath} \begin{array}{rcl} \mathrm{i}^0 q_0(X) + \mathrm{i}^0 q_1(X)... ...mathrm{i}^6 q_2(X)+ \mathrm{i}^9 q_3(X) & = & 0 \\ \end{array}\end{displaymath}$

Da die Matrix 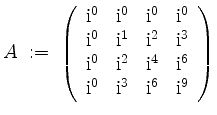$A \; :=\; \left(\begin{array}{rrrr} \mathrm{i}^0 & \mathrm{i}^0 & \mathrm{i}^... ...athrm{i}^0 & \mathrm{i}^3 & \mathrm{i}^6 & \mathrm{i}^9 \\ \end{array}\right)$ unter Verwendung von Zeilenoperationen auf die obere Dreiecksform 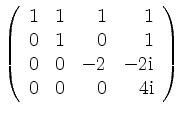$\left(\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & -2 & -2\mathrm{i} \\ 0 & 0 & 0 & 4\mathrm{i} \\ \end{array}\right)$ gebracht werden kann, folgt aus

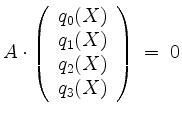
$\displaystyle A\cdot \left(\begin{array}{r} q_0(X) \\ q_1(X) \\ q_2(X) \\ q_3(X) \\ \end{array}\right) \; =\; 0$

daß

für alle $k\in\{0,1,2,3\}$ , und somit die Direktheit der Summe

Insgesamt ist mithin $V = U_0\oplus U_1\oplus U_2\oplus U_3$ gezeigt.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

[Zurück zur Aufgabe]

automatisch erstellt am 11. 8. 2006