
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1311: Orthogonales Komplement |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Sei ![]() , und sei
, und sei
![]() ein Unterraum. Sei
ein Unterraum. Sei
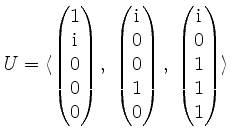 .
Bestimme Orthonormalbasen von
.
Bestimme Orthonormalbasen von
Seien nun
![]() und
und
![]() . Dann gilt für alle
. Dann gilt für alle ![]()
Somit ist
und somit
Sei nun
![]() eine Basis von
eine Basis von ![]() . Wir ergänzen diese zu einer Basis
. Wir ergänzen diese zu einer Basis
![]() von
von
![]() .
Wendet man das Gram-Schmidtsche Orthonormalisierungsverfahren auf dieses Tupel an, so erhält man eine Orthonormalbasis
.
Wendet man das Gram-Schmidtsche Orthonormalisierungsverfahren auf dieses Tupel an, so erhält man eine Orthonormalbasis
![]() von
von
![]() derart, daß
derart, daß
![]() eine Orthonormalbasis von
eine Orthonormalbasis von ![]() ist.
Ferner gilt
ist.
Ferner gilt
![]() für
für ![]() .
.
Also gilt für jedes
![]() und jedes
und jedes
![]() , daß
, daß
und somit
Daraus folgt die Behauptung.
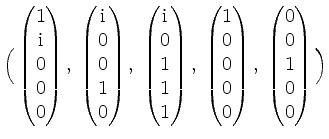 .
Wir wenden das Orthonormalisierungsverfahren von Gram-Schmidt auf diese Basis an. Dies liefert uns dann wie in der Lösung zu 2. die Orthonormalbasen
von
.
Wir wenden das Orthonormalisierungsverfahren von Gram-Schmidt auf diese Basis an. Dies liefert uns dann wie in der Lösung zu 2. die Orthonormalbasen
von
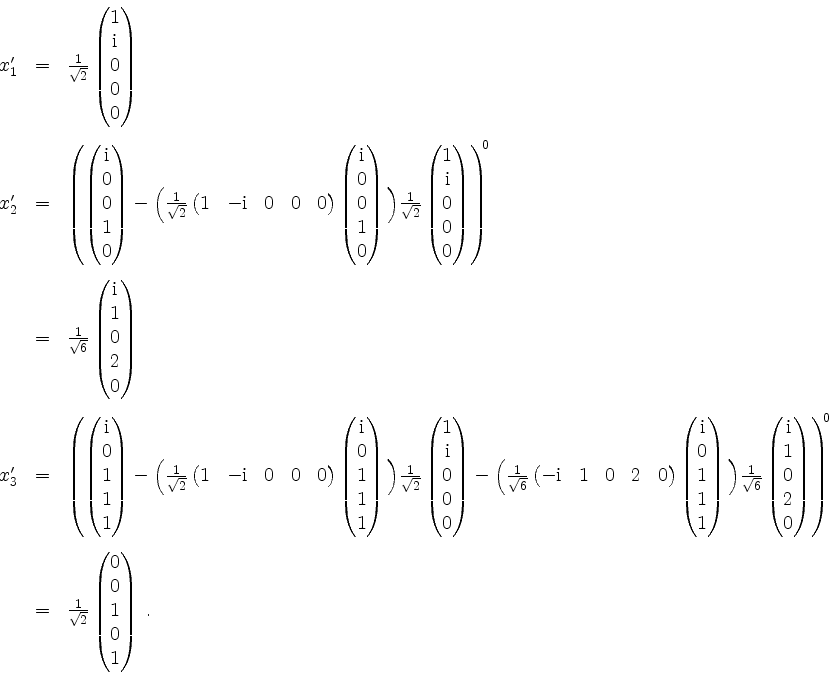
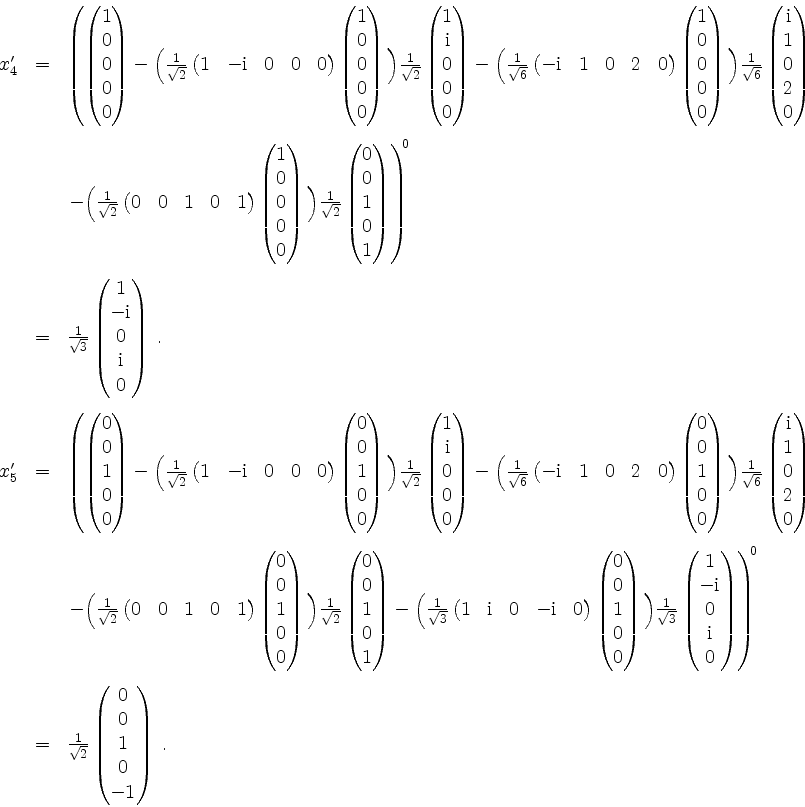
Damit ist
![]() eine Orthonormalbasis von
eine Orthonormalbasis von ![]() , und
, und
![]() eine Orthonormalbasis von
eine Orthonormalbasis von ![]() .
.
| automatisch erstellt am 11. 8. 2006 |