Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1312: Lineare Abbildungen auf Polynomrämen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Betrachte die Abbildungen

\begin{displaymath} \begin{array}{rcl} \mathbb{R}[X] & \longrightarrow & \mathbb... ...mapsto & f(X)^2 \\ f(X) & \mapsto & f(f(X))\;. \\ \end{array}\end{displaymath}

1.
Entscheide, welche Abbildungen dieser Liste linear sind. Begründe jeweils.
2.
Sei $ \mathbb{R}[X]_{\leq 4}$ der Vektorraum über $ \mathbb{R}$ der Polynome von Grad $ \leq 4$ . Sei $ \varphi$ die Summe der linearen Abbildungen dieser Liste, jeweils eingeschränkt zu einem Endomorphismus von $ \mathbb{R}[X]_{\leq 4}$ . Wähle eine Basis von $ \mathbb{R}[X]_{\leq 4}$ und gib die Darstellungsmatrix bezüglich dieser Basis an.
3.
Gib eine Basis von $ \operatorname{Kern}\varphi$ und $ \operatorname{Bild}\varphi$ an. Ist $ \varphi$ injektiv? Ist $ \varphi$ surjektiv?
4.
Gib die Darstellungsmatrix von $ \varphi\circ\varphi$ bezüglich der Basis in 2. an.

1.
Für Polynome $ f(X),\, g(X)\,\in\,\mathbb{R}[X]$ und $ \lambda,\,\mu\,\in\,\mathbb{R}$ gilt

$\displaystyle (\lambda f(X) + \mu g(X))' \;=\; \lambda f'(X)+ \mu g'(X)\;. $

Also ist die Abbildung $ f(X)\mapsto f'(X)$ linear.

Durch Verkettung dieser Abbildung mit sich selbst folgt die Linearität der Abbildung $ f(X)\mapsto f''(X)$ . Verkettet man schließlich die letztere Abbildung mit der Abbildung, welche ein Polynom mit $ X^2$ multipliziert, so erhält man die Linearität der Abbildung $ f(X)\mapsto X^2f''(X)$ .

Verkettung von $ f(X)\mapsto f''(X)$ mit $ g(X)\mapsto g(X^2)$ gibt die Linearität von $ f(X)\mapsto f''(X^2)$ . Hierbei ist wegen

$\displaystyle (\lambda g + \mu h)(X^2) \;=\; \lambda g(X^2)+ \mu h(X^2) $

für $ g(X),\, h(X)\,\in\,\mathbb{R}[X]$ und $ \lambda,\,\mu\,\in\,\mathbb{R}$ die Abbildung $ g(X)\mapsto g(X^2)$ in der Tat linear.

Die Abbildung $ f(X)\mapsto f(X)^2$ ist nicht linear. So z.B. ist $ (1+1)^2 = 4$ , während $ 1^2 + 1^2 = 2$ ist.

Die Abbildung $ f(X)\mapsto f(f(X))$ ist nicht linear. So z.B. $ 2f(X)\mapsto 2f(2f(X))=4f(f(X))$ .

2.
Es wird

$\displaystyle \varphi(f(X)) \;=\; f'(X) + X^2 f''(X) + f''(X^2)\;. $

Somit ist

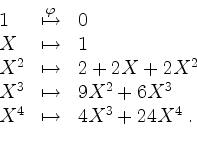
\begin{displaymath} \begin{array}{lcl} 1 &\stackrel{\varphi}{\mapsto} & 0 \\ X ... ...mapsto & 9X^2+6X^3\\ X^4 &\mapsto & 4X^3+24 X^4\;. \end{array}\end{displaymath}

Also ist bezüglich $ \underline{b}:=(1,X,X^2,X^3,X^4)$

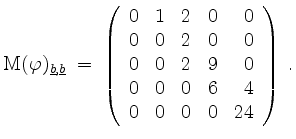
$\displaystyle \mathrm{M}(\varphi)_{\underline{b},\underline{b}} \;=\; \left(\b... ...0 & 2 & 9 & 0\\ 0 & 0 & 0 & 6 & 4\\ 0 & 0 & 0 & 0 & 24 \end{array}\right)\;. $

3.
Die Zeilenstufenform von $ \mathrm{M}(\varphi)_{\underline{b},\underline{b}}$ ist unter Vernachlässigung von Nullzeilen

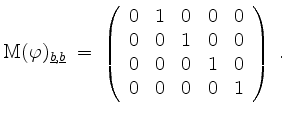
$\displaystyle \mathrm{M}(\varphi)_{\underline{b},\underline{b}} \;=\; \left(\b... ...& 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{array}\right)\;. $

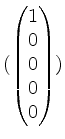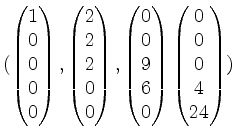Also ist $ (\begin{pmatrix}1\\ 0\\ 0\\ 0\\ 0\end{pmatrix})$ eine Basis von $ \operatorname{Kern }\mathrm{M}(\varphi)_{\underline{b},\underline{b}}$ und $ (\begin{pmatrix}1\\ 0\\ 0\\ 0\\ 0\end{pmatrix},\begin{pmatrix}2\\ 2\\ 2\\ 0\\ ... ...x}0\\ 0\\ 9\\ 6\\ 0\end{pmatrix}\begin{pmatrix}0\\ 0\\ 0\\ 4\\ 24\end{pmatrix})$ eine Basis von $ \operatorname{Bild} \mathrm{M}(\varphi)_{\underline{b},\underline{b}}$ .

Folglich ist $ (1)$ ($ = (X^0)$ ) eine Basis von $ \operatorname{Kern}\varphi$ und $ (1, 2+2X+2X^2, 9X^2+6X^3, 4X^3+24X^4)$ eine Basis von $ \operatorname{Bild}\varphi$ .

Da $ \dim\operatorname{Kern}\varphi=1>0$ ist, ist $ \varphi$ nicht injektiv. Da $ \dim\operatorname{Bild}\varphi=4<5$ ist, ist $ \varphi$ nicht surjektiv.

4.
Es ist

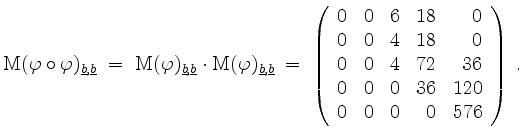
$\displaystyle \mathrm{M}(\varphi\circ\varphi)_{\underline{b},\underline{b}} \;=... ...& 72 & 36\\ 0 & 0 & 0 & 36 & 120\\ 0 & 0 & 0 & 0 & 576 \end{array}\right)\;. $

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 22.  8. 2006