Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1313: Inverse von oberen Dreiecksmatrizen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei $ K$ ein Körper.

1.
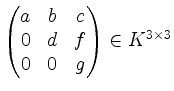Seien $ a,\, d,\, g\,\in\, K\setminus\{ 0\}$ , seien $ b,\, c,\, f\,\in\, K$ . Berechne die Inverse zu $ \begin{pmatrix}a&b&c\\ 0&d&f\\ 0&0&g\end{pmatrix}\in K^{3\times 3}$ .
2.
Seien $ r,\, s,\, t\,\geq\, 1$ . Seien $ A\in K^{r\times r}$ , $ D\in K^{s\times s}$ und $ G\in K^{t\times t}$ invertierbar, seien $ B\in K^{r\times s}$ , $ C\in K^{r\times t}$ und $ F\in K^{s\times t}$ beliebig. Bestimme die Inverse der Blockmatrix

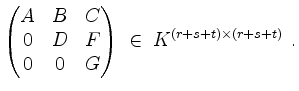
$\displaystyle \begin{pmatrix}A&B&C\\ 0&D&F\\ 0&0&G\end{pmatrix} \;\in\; K^{(r+s+t)\times (r+s+t)}\; . $

1.
Wir setzen an

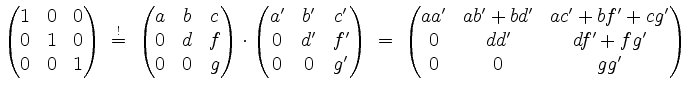
$\displaystyle \begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}\; \stackrel{ !}... ...; \begin{pmatrix}aa'&ab'+bd'&ac'+bf'+cg'\\ 0&dd'&df'+fg'\\ 0&0&gg'\end{pmatrix}$

mit $ a',b',c',d',f',g'\in K$ .

Die Gleichungen

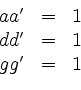
\begin{displaymath} \begin{array}{rcl} aa' &=& 1\\ dd' &=& 1\\ gg' &=& 1 \end{array}\end{displaymath}

liefern

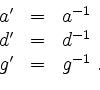
\begin{displaymath} \begin{array}{rcl} a' &=& a^{-1}\\ d' &=& d^{-1}\\ g' &=& g^{-1}\;. \end{array}\end{displaymath}

Dann liefern die Gleichungen

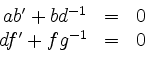
\begin{displaymath} \begin{array}{rcl} ab'+bd^{-1} &=& 0\\ df'+fg^{-1} &=& 0 \end{array}\end{displaymath}

die Lösung

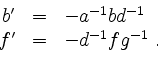
\begin{displaymath} \begin{array}{rcl} b' &=& -a^{-1}bd^{-1}\\ f' &=& -d^{-1}fg^{-1}\;. \end{array}\end{displaymath}

Schließlich folgt aus

$\displaystyle ac' + bf' + cg' \;=\; ac'-bd^{-1}fg^{-1}+cg^{-1} \;=\; 0 \;, $

daß

$\displaystyle c' \;=\; a^{-1}(bd^{-1}f-c)g^{-1} \;. $

Damit ist

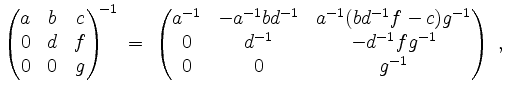
$\displaystyle \begin{pmatrix}a&b&c\\ 0&d&f\\ 0&0&g\end{pmatrix}^{\!\!-1} \;=\; ... ...^{-1}(bd^{-1}f-c)g^{-1}\\ 0&d^{-1}&-d^{-1}fg^{-1}\\ 0&0&g^{-1}\end{pmatrix}\;, $

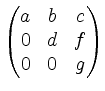wie man durch Multiplikation mit $ \begin{pmatrix}a&b&c\\ 0&d&f\\ 0&0&g\end{pmatrix}$ verifiziert.

2.
Wir setzen an

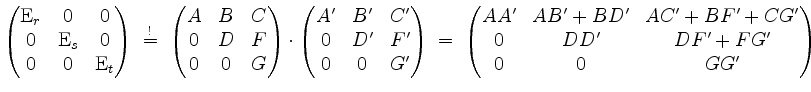
$\displaystyle \begin{pmatrix}\mathrm{E}_r&0&0\\ 0&\mathrm{E}_s&0\\ 0&0&\mathrm{... ...; \begin{pmatrix}AA'&AB'+BD'&AC'+BF'+CG'\\ 0&DD'&DF'+FG'\\ 0&0&GG'\end{pmatrix}$

mit $ A'\in K^{r\times r}$ , $ D'\in K^{s\times s}$ , $ G'\in K^{t\times t}$ , $ B'\in K^{r\times s}$ , $ C'\in K^{r\times t}$ und $ F'\in K^{s\times t}$ .

Die Gleichungen

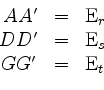
\begin{displaymath} \begin{array}{rcl} AA' &=& \mathrm{E}_r\\ DD' &=& \mathrm{E}_s\\ GG' &=& \mathrm{E}_t \end{array}\end{displaymath}

liefern

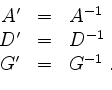
\begin{displaymath} \begin{array}{rcl} A' &=& A^{-1}\\ D' &=& D^{-1}\\ G' &=& G^{-1}\;. \end{array}\end{displaymath}

Dann liefern die Gleichungen

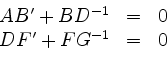
\begin{displaymath} \begin{array}{rcl} AB'+BD^{-1} &=& 0\\ DF'+FG^{-1} &=& 0 \end{array}\end{displaymath}

die Lösung

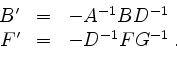
\begin{displaymath} \begin{array}{rcl} B' &=& -A^{-1}BD^{-1}\\ F' &=& -D^{-1}FG^{-1}\;. \end{array}\end{displaymath}

Schließlich folgt aus

$\displaystyle AC' + BF' + CG' \;=\; AC'-BD^{-1}FG^{-1}+CG^{-1} \;=\; 0 \;, $

daß

$\displaystyle C' \;=\; A^{-1}(BD^{-1}F-C)G^{-1} \;. $

Damit ist

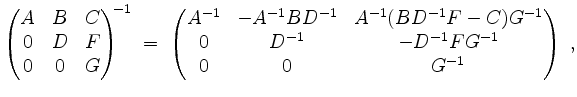
$\displaystyle \begin{pmatrix}A&B&C\\ 0&D&F\\ 0&0&G\end{pmatrix}^{\!\!-1} \;=\; ... ...^{-1}(BD^{-1}F-C)G^{-1}\\ 0&D^{-1}&-D^{-1}FG^{-1}\\ 0&0&G^{-1}\end{pmatrix}\;, $

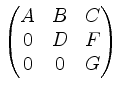wie man durch Multiplikation mit $ \begin{pmatrix}A&B&C\\ 0&D&F\\ 0&0&G\end{pmatrix}$ verifiziert.
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006