
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1317: Berechnung der Jordanform |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Sei
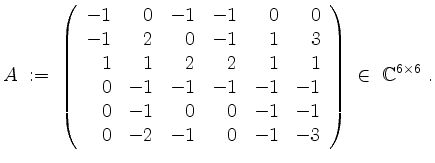
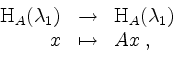
wobei
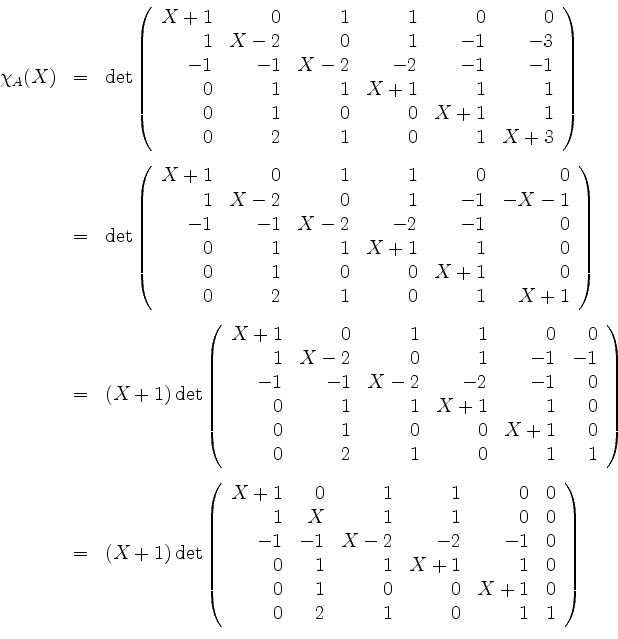
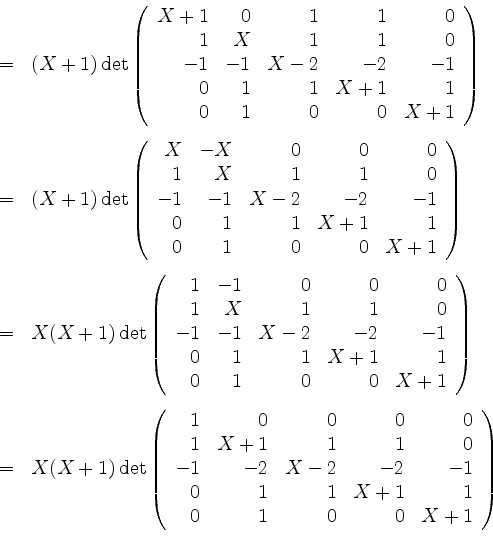
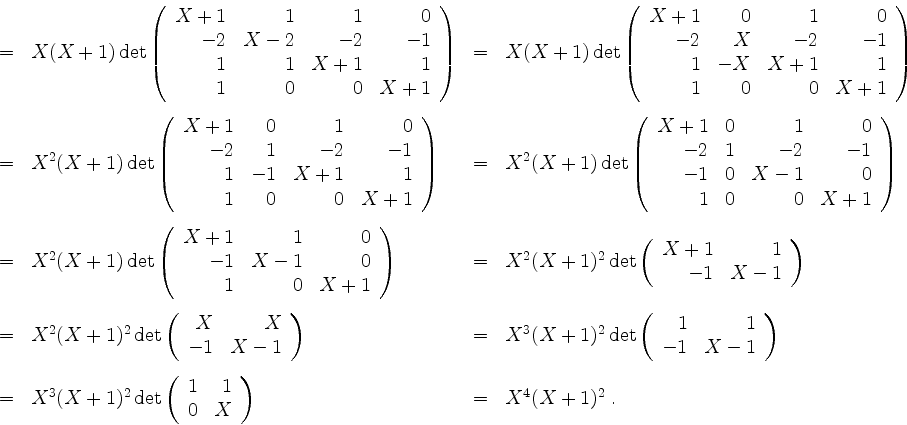
Die Eigenwerte von ![]() sind
sind
![]() mit algebraischer Vielfachheit vier und
mit algebraischer Vielfachheit vier und
![]() mit algebraischer Vielfachheit zwei.
mit algebraischer Vielfachheit zwei.
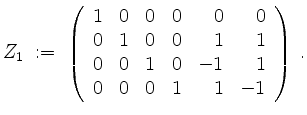
Wir erhalten als Basis von
![]()
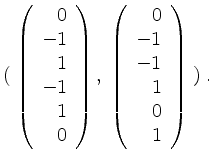
Nun bringen wir ![]() auf Zeilenstufenform
auf Zeilenstufenform
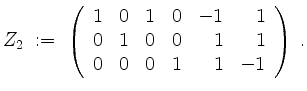
Position
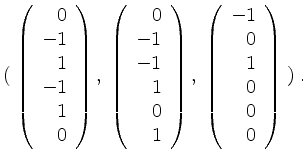
Nun bringen wir ![]() auf Zeilenstufenform
auf Zeilenstufenform
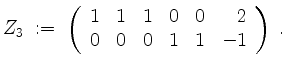
Position
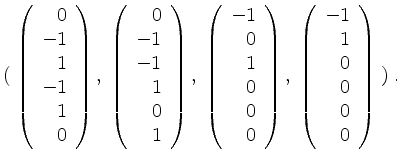
Nun ist
Das Tableau zu
![]() sieht also vor der Kettenbildung wie folgt aus.
sieht also vor der Kettenbildung wie folgt aus.
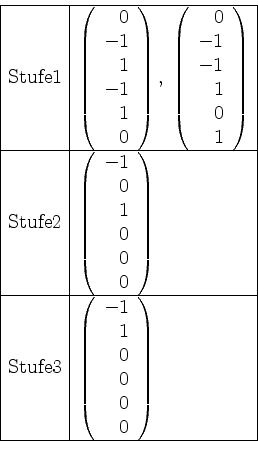
Nun bilden wir den Vektor in Stufe
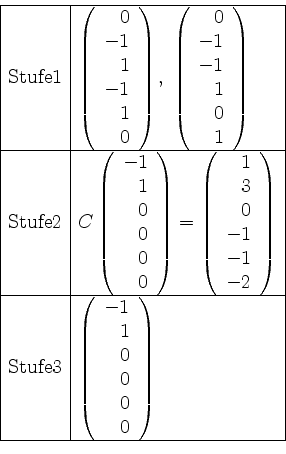
Nun bilden wir den Vektor in Stufe
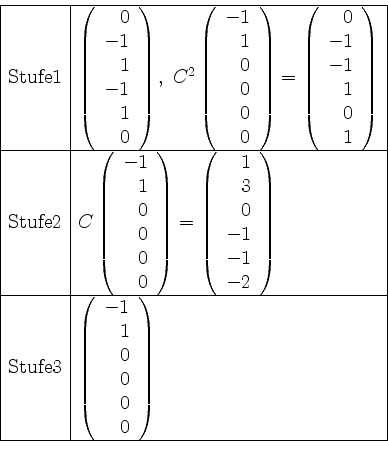
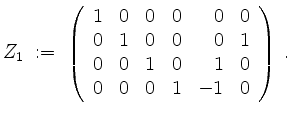
Wir erhalten als Basis von
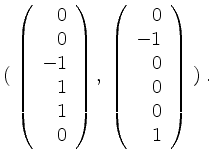
Nun ist
Das Tabelau zum Hauptraum
![]() sieht also wie folgt aus.
sieht also wie folgt aus.
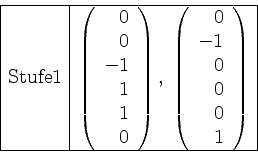
Der zweite Schritt, die Kettenbildung, entfällt hier.
Zusammensetzen der Bestandteile liefert die Kettenbasis von
![]() , und somit
, und somit
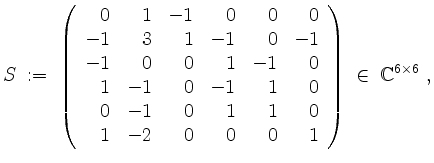
sowie
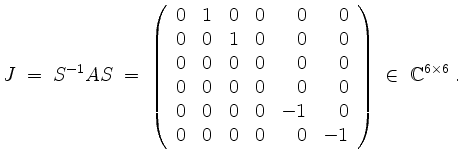
Anstatt
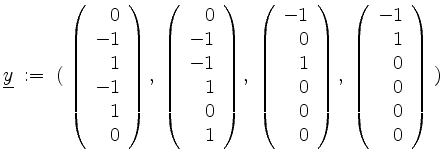
von
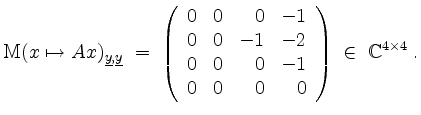
Dies ist eine obere Blockdreiecksmatrix mit Hauptdiagonalblöcken
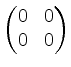 ,
,
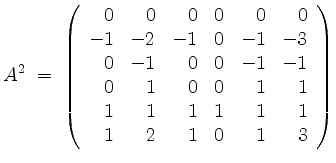
an. Denn es ist
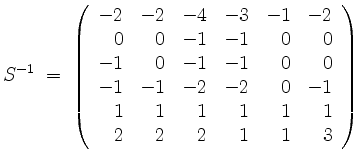
das Resultat
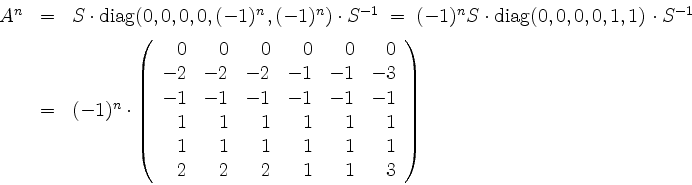
für
| automatisch erstellt am 22. 8. 2006 |