Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1318: Rekursiv definierte Folgen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei $ (a_n)_{n\geq 0}$ eine rekursiv definierte Folge. Berechne das Folgenglied $ a_n$ direkt.

1.
Seien $ a_1 = 0$ , $ a_2 = 1$ und $ a_n = a_{n-1} + a_{n-2}$ für $ n\geq 3$ (Fibonacci).
2.
Seien $ a_1 = 0$ , $ a_2 = 0$ , $ a_3 = 1$ , $ a_4 = 1$ und $ a_n = 2a_{n-2} - a_{n-4}$ für $ n\geq 5$ .

1.
Die rekursive Definition kann unter Zuhilfenahme der Matrixmultiplikation geschrieben werden als

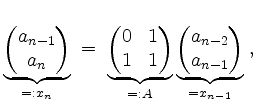
$\displaystyle \underbrace{\begin{pmatrix}a_{n-1}\\ a_n\end{pmatrix}}_{=: x_n} \... ... A} \underbrace{\begin{pmatrix}a_{n-2}\\ a_{n-1}\end{pmatrix}}_{= x_{n-1}}\; , $

für $ n\geq 3$ .

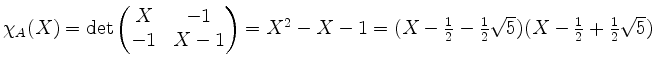Wir erhalten $ \chi_A(X) = \det\begin{pmatrix}X&-1\\ -1&X-1\end{pmatrix} = X^2 - X - 1 = (X - \frac{1}{2} - \frac{1}{2}\sqrt{5})(X - \frac{1}{2} + \frac{1}{2}\sqrt{5})$ .

Es wird

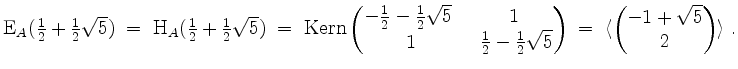
$\displaystyle \mathrm{E}_A({\textstyle\frac{1}{2} + \frac{1}{2}\sqrt{5}}) \;=\;... ...d{pmatrix}\;=\; \langle\begin{pmatrix}-1+\sqrt{5} \\ 2\end{pmatrix}\rangle\; . $

Dies ist der Beitrag von $ \mathrm{H}_A({\textstyle\frac{1}{2} + \frac{1}{2}\sqrt{5}})$ zu den Spalten von $ S$ .

Ferner wird

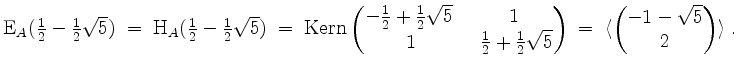
$\displaystyle \mathrm{E}_A({\textstyle\frac{1}{2} - \frac{1}{2}\sqrt{5}}) \;=\;... ...nd{pmatrix}\;=\; \langle\begin{pmatrix}-1-\sqrt{5}\\ 2\end{pmatrix}\rangle\; . $

Dies ist der Beitrag von $ \mathrm{H}_A({\textstyle\frac{1}{2} + \frac{1}{2}\sqrt{5}})$ zu den Spalten von $ S$ .

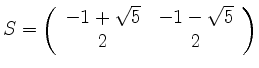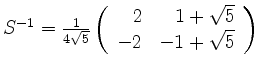Mit $ S = \left(\begin{array}{cc}-1+\sqrt{5}&-1-\sqrt{5}\\ 2 & 2\end{array}\right)$ wird $ S^{-1} = \frac{1}{4\sqrt{5}} \left(\begin{array}{rr}2 & 1+\sqrt{5}\\ -2& -1+\sqrt{5}\end{array}\right)$ und

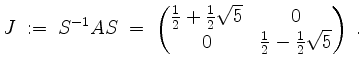
$\displaystyle J \; :=\; S^{-1}AS \;=\; \begin{pmatrix}\frac{1}{2} + \frac{1}{2}\sqrt{5} & 0\\ 0 & \frac{1}{2} - \frac{1}{2}\sqrt{5}\end{pmatrix}\;. $

Damit wird

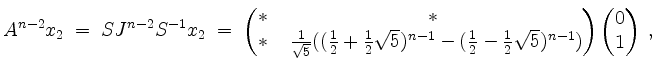
$\displaystyle A^{n-2} x_2 \;=\; SJ^{n-2}S^{-1}x_2 \;=\; \begin{pmatrix}\ast&\a... ...ac{1}{2}\sqrt{5})^{n-1}) \end{pmatrix} \begin{pmatrix}0 \\ 1\end{pmatrix}\; , $

und also

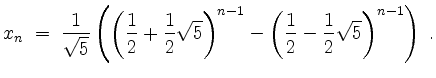
$\displaystyle x_n \;=\; \frac{1}{\sqrt{5}}\left(\left(\frac{1}{2} + \frac{1}{2}... ...right)^{n-1} - \left(\frac{1}{2} - \frac{1}{2}\sqrt{5}\right)^{n-1}\right)\; . $

2.
Die rekursive Definition kann unter Zuhilfenahme der Matrixmultiplikation geschrieben werden als

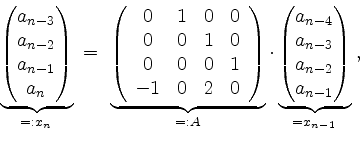
\begin{displaymath} \underbrace{\begin{pmatrix}a_{n-3}\\ a_{n-2}\\ a_{n-1}\\ a_{... ...4}\\ a_{n-3}\\ a_{n-2}\\ a_{n-1}\end{pmatrix}}_{= x_{n-1}}\; , \end{displaymath}

für $ n\geq 5$ .

Wir erhalten

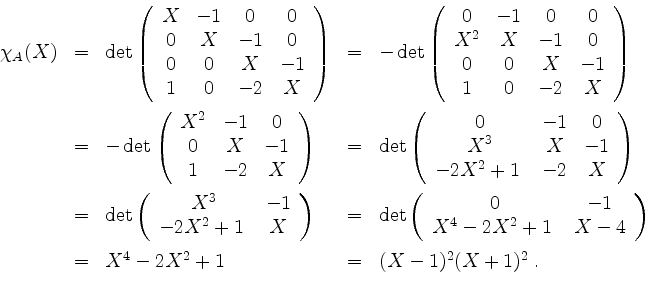
\begin{displaymath} \begin{array}{rclcl} \chi_A(X) & = & \det\left( \begin{arra... ...= & X^4 - 2X^2 + 1 & = & (X - 1)^2(X + 1)^2\; . \\ \end{array}\end{displaymath}

(Eigenwert $ 1$ )
Wir bringen die Matrix $ C:=A-\mathrm{E}$ auf Zeilenstufenform und erhalten

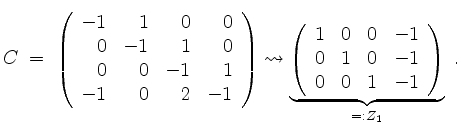
$\displaystyle C\;=\; \left(\begin{array}{rrrr} -1 & 1 & 0 & 0\\ 0 &-1 & 1 & 0\... ...1 & 0 & 0 &-1\\ 0 & 1 & 0 &-1\\ 0 & 0 & 1 &-1 \end{array}\right)}_{=:Z_1}\;. $

Also ist eine Basis von $ \operatorname{Kern }C$ gegeben durch

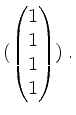
$\displaystyle (\begin{pmatrix}1\\ 1\\ 1\\ 1\end{pmatrix})\;. $

Nun bringen wir die Matrix $ Z_1C$ auf Zeilenstufenform und erhalten

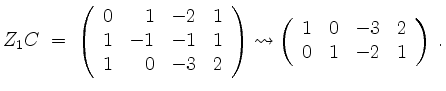
$\displaystyle Z_1C\;=\; \left(\begin{array}{rrrr} 0 & 1 &-2 & 1\\ 1 &-1 &-1 & ... ...\left(\begin{array}{rrrr} 1 & 0 &-3 & 2\\ 0 & 1 &-2 & 1 \end{array}\right)\;. $

Also können wir die Basis von $ \operatorname{Kern }C$ ergänzen zu einer Basis

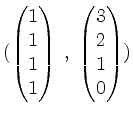
$\displaystyle (\begin{pmatrix}1\\ 1\\ 1\\ 1\end{pmatrix}\;,\;\begin{pmatrix}3\\ 2\\ 1\\ 0\end{pmatrix}) $

von $ \operatorname{Kern}(C^2)=\operatorname{Kern}(Z_1C)$ . Da die Dimension des Hauptraums $ \mathrm{H}_A(1)$ mit der Dimension von $ \operatorname{Kern}(C^2)$ übereinstimmt, haben wir bereits eine Basis von $ \mathrm{H}_A(1)$ gefunden. Das Tableau zu $ \mathrm{H}_A(1)$ sieht vor der Kettenbildung also wie folgt aus.

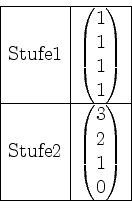
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe }1 & ... ... \begin{pmatrix}3\\ 2\\ 1\\ 0\end{pmatrix}\\ \hline \end{array}\end{displaymath}

Nun bilden wir den Vektor in Stufe $ 2$ mittels $ C$ ab, tragen ihn in Stufe $ 1$ ein, und streichen den schon vorhandenen Vektor in Stufe $ 1$ aus Dimensionsgründen.

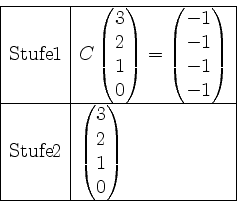
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe }1 & ... ... \begin{pmatrix}3\\ 2\\ 1\\ 0\end{pmatrix}\\ \hline \end{array}\end{displaymath}

(Eigenwert $ -1$ )
Wir bringen die Matrix $ C:=A+\mathrm{E}$ auf Zeilenstufenform und erhalten

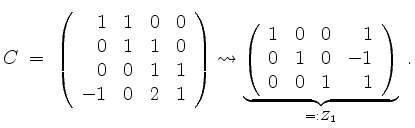
$\displaystyle C\;=\; \left(\begin{array}{rrrr} 1 & 1 & 0 & 0\\ 0 & 1 & 1 & 0\\... ...1 & 0 & 0 & 1\\ 0 & 1 & 0 &-1\\ 0 & 0 & 1 & 1 \end{array}\right)}_{=:Z_1}\;. $

Also ist eine Basis von $ \operatorname{Kern }C$ gegeben durch

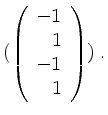
$\displaystyle (\left(\begin{array}{r} -1\\ 1\\ -1\\ 1\end{array}\right))\;. $

Nun bringen wir die Matrix $ Z_1C$ auf Zeilenstufenform und erhalten

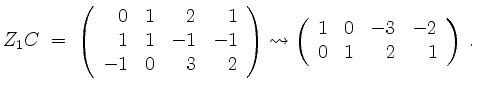
$\displaystyle Z_1C\;=\; \left(\begin{array}{rrrr} 0 & 1 & 2 & 1\\ 1 & 1 &-1 &-... ...\left(\begin{array}{rrrr} 1 & 0 &-3 &-2\\ 0 & 1 & 2 & 1 \end{array}\right)\;. $

Also können wir die Basis von $ \operatorname{Kern }C$ ergänzen zu einer Basis

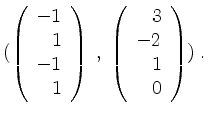
$\displaystyle (\left(\begin{array}{r} -1\\ 1\\ -1\\ 1\end{array}\right)\;,\; \left(\begin{array}{r} 3\\ -2\\ 1\\ 0\end{array}\right))\;. $

von $ \operatorname{Kern}(C^2)=\operatorname{Kern}(Z_1C)$ . Da die Dimension des Hauptraums $ \mathrm{H}_A(-1)$ mit der Dimension von $ \operatorname{Kern}(C^2)$ übereinstimmt, haben wir bereits eine Basis von $ \mathrm{H}_A(-1)$ gefunden. Das Tableau zu $ \mathrm{H}_A(-1)$ sieht vor der Kettenbildung also wie folgt aus.

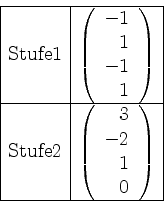
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe }1 & ... ...{array}{r}3\\ -2\\ 1\\ 0\end{array}\right)\\ \hline \end{array}\end{displaymath}

Nun bilden wir den Vektor in Stufe $ 2$ mittels $ C$ ab, tragen ihn in Stufe $ 1$ ein, und streichen den schon vorhandenen Vektor in Stufe $ 1$ aus Dimensionsgründen.

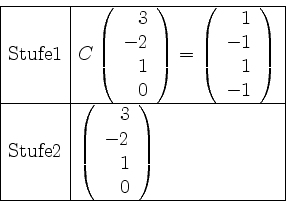
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe }1 & ... ...{array}{r}3\\ -2\\ 1\\ 0\end{array}\right)\\ \hline \end{array}\end{displaymath}

Nun können wir die beiden Kettenbasen als Spalten in die Matrix $ S$ eintragen.

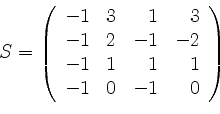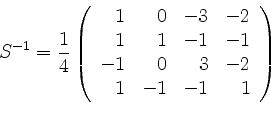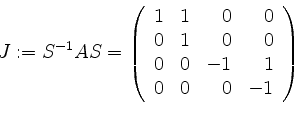Mit \begin{displaymath}S = \left( \begin{array}{rrrr} -1 & 3 & 1 & 3 \\ -1 & 2 &... ...\\ -1 & 1 & 1 & 1 \\ -1 & 0 & -1 & 0 \\ \end{array}\right)\end{displaymath} wird \begin{displaymath}S^{-1} = \frac{1}{4} \left( \begin{array}{rrrr} 1 & 0 & -3 &... ...\ -1 & 0 & 3 & -2 \\ 1 & -1 & -1 & 1 \\ \end{array}\right)\end{displaymath} und \begin{displaymath}J := S^{-1} A S = \left( \begin{array}{rrrr} 1 & 1 & 0 & 0 ... ...\\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & -1 \\ \end{array}\right) \end{displaymath} .

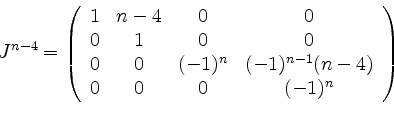Da nun \begin{displaymath}J^{n - 4} = \left( \begin{array}{cccc} 1 & n-4 & 0 & 0 \\ ... ... (-1)^{n-1}(n-4) \\ 0 & 0 & 0 & (-1)^n \\ \end{array}\right)\end{displaymath} , wird

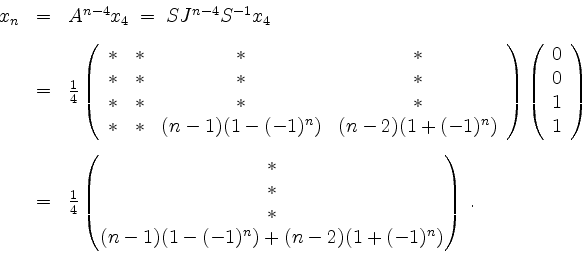
\begin{displaymath} \begin{array}{rcl} x_n &=& A^{n - 4} x_4 \;=\; S J^{n-4} S^... ...(1 - (-1)^n) + (n-2) ( 1 + (-1)^n)\end{pmatrix}\; . \end{array}\end{displaymath}

In anderen Worten,

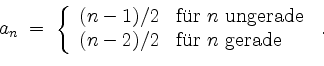
\begin{displaymath} a_n \;=\; \left\{ \begin{array}{ll} (n - 1)/2 & \mbox{f''ur ... ... - 2)/2 & \mbox{f''ur $n$\ gerade} \\ \end{array}\right. \; . \end{displaymath}

Das sieht man auch, ohne Matrizen heranzuziehen. Im allgemeinen ist dies jedoch bei solchen Rekursionsaufgaben schwierig.
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 22.  8. 2006