Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1320: Definitheit und unitäre Diagonalisierung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei

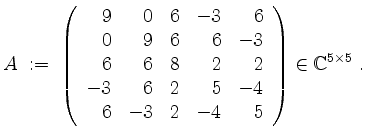
$\displaystyle A \;:=\; \left(\begin{array}{rrrrr} 9& 0& 6& -3& 6\\ 0& 9& 6& 6&... ... 6& 2& 5& -4\\ 6& -3& 2& -4& 5 \end{array}\right)\in\mathbb{C}^{5\times 5}\;. $

1.
Kann man durch bloßes Betrachten der Matrix ausschließen, daß $ A$ positiv semidefinit ist oder daß $ A$ negativ semidefinit ist?

2.
Untersuche $ A$ mittels Hauptminoren auf Definitheit.

3.
Untersuche $ A$ mittels charakteristischem Polynom auf Definitheit.

4.
Berechne die Signatur von $ A$ mittels beidseitigem Gaußschen Algorithmus.

5.
Diagonalisiere $ A$ unitär.

1.
Da die Einträge auf der Hauptdiagonalen nicht sämtlich $ \leq 0$ sind, ist $ A$ nicht negativ semidefinit. Positive Semidefinitheit kann man nicht ausschließen, aber an dieser Stelle auch noch nicht bestätigen.

2.
Die Hauptminoren ergeben sich zu $ \det A_1=9$ , $ \det A_2=81$ , $ \det A_3=\det A_4 = \det A_5 =0$ . Daraus folgt, daß $ A$ nicht positiv definit und nicht negativ definit ist.

3.
Es wird

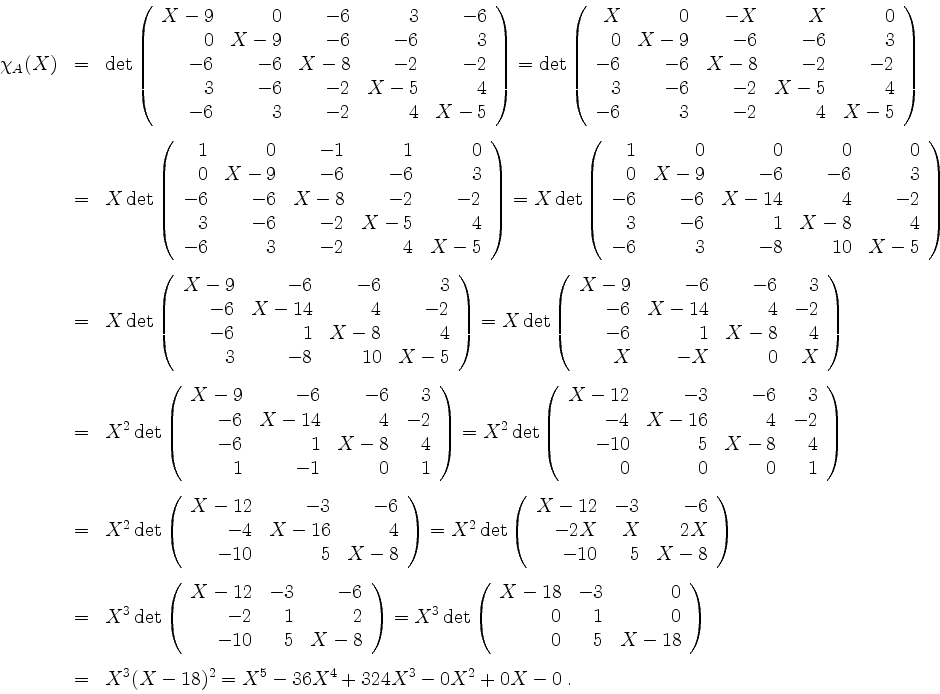
\begin{displaymath} \begin{array}{rclcl} \chi_A(X) \par &=& \det\left(\begin{ar... ...=& X^3(X-18)^2 \par = X^5-36X^4+324X^3-0X^2+0X-0\;. \end{array}\end{displaymath}

Damit ist $ A$ positiv semidefinit, weil die Koeffizienten abwechselndes Vorzeichen haben oder 0 sind.

Tatsächlich haben wir hier die Eigenwerte 0 und $ 18$ von $ A$ berechnet, was ebenfalls positive Semidefinitheit nach sich zieht. Sogar die Signatur $ (2,0)$ kann abgelesen werden. Dies wäre allerdings schwierig, wenn $ \chi_A(X)$ nicht in faktorisierter Form hätte gefunden werden können.

4.
Mittels beidseitigem Gaußschen Algorithmus ergibt sich

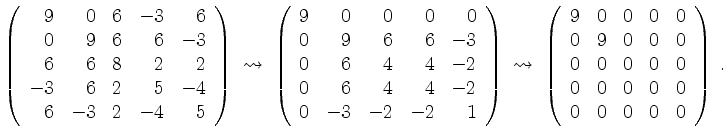
$\displaystyle \left(\begin{array}{rrrrr} 9& 0& 6& -3& 6\\ 0& 9& 6& 6& -3\\ 6&... ... 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0 \end{array}\right)\;. $

Also ist die Signatur von $ A$ gleich $ (2,0)$ .

5.
Es ergibt sich

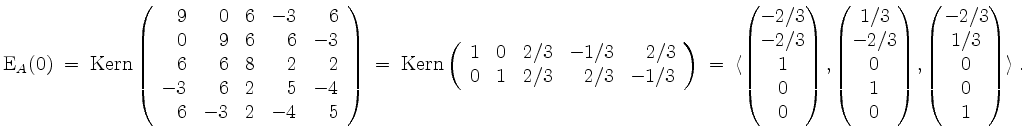
$\displaystyle \mathrm{E}_A(0) \;=\; \mathrm{Kern }\left(\begin{array}{rrrrr} 9... ...\\ 0\end{pmatrix},\begin{pmatrix}-2/3\\ 1/3\\ 0\\ 0\\ 1\end{pmatrix}\rangle\;. $

Gram-Schmidt ergibt für $ \mathrm{E}_A(0)$ die Orthonormalbasis

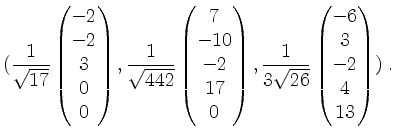
$\displaystyle (\frac{1}{\sqrt{17}}\begin{pmatrix}-2\\ -2\\ 3\\ 0\\ 0\end{pmatri... ...trix},\frac{1}{3\sqrt{26}}\begin{pmatrix}-6\\ 3\\ -2\\ 4\\ 13\end{pmatrix})\;. $

Ferner wird

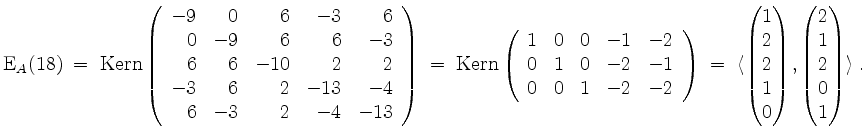
$\displaystyle \mathrm{E}_A(18) \;=\; \mathrm{Kern }\left(\begin{array}{rrrrr} ... ...2\\ 1\\ 0\end{pmatrix},\begin{pmatrix}2\\ 1\\ 2\\ 0\\ 1\end{pmatrix}\rangle\;. $

Gram-Schmidt ergibt für $ \mathrm{E}_A(18)$ die Orthonormalbasis

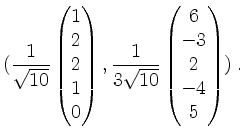
$\displaystyle (\frac{1}{\sqrt{10}}\begin{pmatrix}1\\ 2\\ 2\\ 1\\ 0\end{pmatrix}, \frac{1}{3\sqrt{10}}\begin{pmatrix}6\\ -3\\ 2\\ -4\\ 5\end{pmatrix})\;. $

Damit erhalten wir die unitäre Matrix

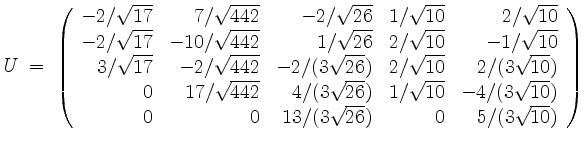
$\displaystyle U \;=\; \left(\begin{array}{rrrrr} -2/\sqrt{17}& 7/\sqrt{442}& -... ...sqrt{10})\\ 0 & 0 & 13/(3\sqrt{26})& 0 & 5/(3\sqrt{10})\\ \end{array}\right) $

und somit

$\displaystyle \bar{U}^\mathrm{t} AU \;=\; \mathrm{diag}(0,0,0,18,18)\;. $

Dieses Standardverfahren liefert i.a. nicht die einfachsten Zahlenwerte. Zum Beispiel ergibt sich auch mit

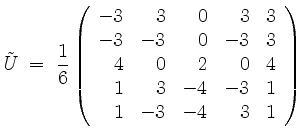
$\displaystyle \tilde{U} \;=\; \frac{1}{6}\left(\begin{array}{rrrrr} -3& 3& 0& ... ...3& 3\\ 4& 0& 2& 0& 4\\ 1& 3& -4& -3& 1\\ 1& -3& -4& 3& 1 \end{array}\right) $

die unitäre Diagonalisierung

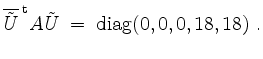
$\displaystyle \overline{\tilde{U}}^{\;\mathrm{t}} A\tilde{U} \;=\; \mathrm{diag}(0,0,0,18,18)\;. $

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006