Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1323: Abgeschlossene und kompakte Mengen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1.
Sei $ f:\mathbb{R}^n\to\mathbb{R}$ eine stetige Funktion und seien $ -\infty\leq a\leq b\leq\infty$ . Zeige, daß die Menge $ A=\{x\in\mathbb{R}^n\vert\; a\leq f(x)\leq b\}$ abgeschlossen ist.
2.
Zeige, daß die $ n$ -dimensionale Kugel $ K=\{x\in\mathbb{R}^n\vert\; \Vert x\Vert\leq 1\}$ und ihre Oberfläche $ O=\{x\in\mathbb{R}^n\vert\; \Vert x\Vert=1\}$ jeweils kompakt sind.
3.
Zeige, daß die Menge $ K=\{(\frac{\cos x}{x}\;,\;\frac{\sin x}{x})^\mathrm{t}\in\mathbb{R}^2\vert\; x\geq 2\pi\} \cup\{(0,0)^\mathrm{t}\}$ kompakt ist.
1.
Sei $ (x_k)_{k\ge 1}$ eine konvergente Folge mit $ x_k\in A$ für alle $ k\ge 1$ und $ x_0=\lim\limits_{k\to\infty} x_k$ .

Da $ f$ stetig ist, folgt $ f(x_k)\to f(x_0)$ für $ k\to\infty$ . Ferner gilt $ a\leq f(x_k)\leq b$ für alle $ k\ge 1$ . Für $ k\to\infty$ folgt daher $ a\leq f(x_0)\leq b$ , d.h. $ x_0\in A$ .

Damit haben wir gezeigt, daß die Menge $ A$ alle ihre Berührpunkte enthält, d.h. sie ist abgeschlossen.

2.
Die Beschränktheit beider Mengen folgt direkt aus ihren Definitionen.

Betrachte nun die Funktion $ f:\mathbb{R}^n\to\mathbb{R},\; x\mapsto \Vert x\Vert$ . Dann gilt

$\displaystyle K\; =\;\{x\in\mathbb{R}^n\;\vert\; 0\leq f(x)\leq 1\}\; ,\;\; O\; =\;\{x\in\mathbb{R}^n\;\vert\; 1\leq f(x)\leq 1\}\;. $

Nach Aufgabenteil 1. sind $ K$ und $ O$ somit abgeschlossen. Insgesamt sind sie also kompakt.

3.
Zunächst gilt

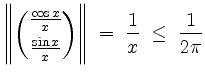
$\displaystyle \left\Vert{\frac{\cos x}{x}\choose\frac{\sin x}{x}}\right\Vert \;=\; \frac{1}{x} \;\leq\; \frac{1}{2\pi} $

für alle $ x\geq 2\pi$ . Daher ist die Menge $ K$ beschränkt.

Sei nun $ (a,b)^\mathrm{t}\in\mathbb{R}^2$ ein Berührpunkt von $ K$ . Wir wollen zeigen, daß $ (a,b)^\mathrm{t} \in K$ ist.

Sei dazu $ (c_k)_{k\ge 1}$ eine konvergente Folge mit $ c_k\in K$ und $ \lim_{k\to\infty} c_k=(a,b)^\mathrm{t}$ . Wir können ohne Einschränkung annehmen, daß $ (a,b)^\mathrm{t}\ne(0,0)^\mathrm{t}$ und $ c_k\ne(0,0)^\mathrm{t}$ für alle $ k\ge 1$ . Es ist also $ c_k=(\frac{\cos x_k}{x_k}\;,\;\frac{\sin x_k}{x_k})^\mathrm{t}$ für gewisse $ x_k \geq 2\pi$ .

Da die Folge $ (c_k)_{k\ge 1}$ in $ \mathbb{R}^2\setminus\{ 0\}$ konvergiert, existiert der Grenzwert

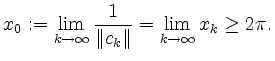
$\displaystyle x_0 := \lim\limits_{k \to \infty} \frac{1}{\Vert c_k\Vert} = \lim\limits_{k \to \infty} x_k \geq 2\pi. $

Daraus folgt

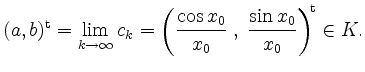
$\displaystyle (a,b)^\mathrm{t} = \lim\limits_{k \to \infty} c_k = \left(\frac{\cos x_0}{x_0}\;,\;\frac{\sin x_0}{x_0}\right)^{\! \mathrm{t}} \in K. $

Also enthält $ K$ alle seine Berührpunkte und ist somit abgeschlossen und beschränkt.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006