Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1324: Jacobimatrix von Koordinatentransformationen und ihre Determinante

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

1.
Berechne jeweils die Jacobimatrix von $ f$ und deren Determinante. Ist $ f$ differenzierbar?

(a)
$ f: \mathbb{R}^2 \to \mathbb{R}^2,\; (r, \varphi)^\mathrm{t} \mapsto (r \cos \varphi, r \sin \varphi)^\mathrm{t}$ (Polarkoordinaten).
(b)
$ f: \mathbb{R}^3 \to \mathbb{R}^3,\; (r, \varphi, z)^\mathrm{t} \mapsto (r \cos \varphi, r \sin \varphi, z)^\mathrm{t}$ (Zylinderkoordinaten).
(c)
$ f: \mathbb{R}^3 \to \mathbb{R}^3,\; (r,\varphi,\psi)^\mathrm{t} \mapsto (r (\sin\varphi) (\cos\psi), r(\sin\varphi) (\sin\psi), r \cos\varphi)^\mathrm{t}$ (Kugelkoordinaten).

2.
Es sei $ f: \mathbb{R}^2 \to \mathbb{R}$ zweimal stetig differenzierbar. Die Transformation in Polarkoordinaten liefert eine Funktion $ F(r, \varphi) := f(r \cos \varphi, r \sin \varphi)$.

Berechne alle partiellen Ableitungen erster und zweiter Ordnung von $ F$. Zeige, daß im Punkt $ (x,y)^\mathrm{t} = (r \cos \varphi, r \sin \varphi)^\mathrm{t} \in \mathbb{R}^2\setminus\{0\}$ folgendes gilt.

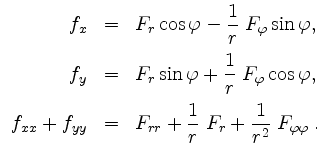
$\displaystyle \begin{array}{rcl} f_x & = & F_r \cos \varphi - \dfrac{1}{r}\; F_... ...+ \dfrac{1}{r}\; F_r + \dfrac{1}{r^2}\; F_{\varphi \varphi} \; .\\ \end{array}$

1.
(a)
Wir berechnen

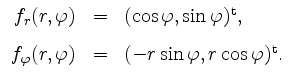
$\displaystyle \begin{array}{rcl} f_r(r,\varphi) & = & (\cos \varphi, \sin \varp... ...phi(r,\varphi) & = & (- r \sin \varphi, r \cos \varphi)^\mathrm{t}. \end{array}$

Die partiellen Ableitungen sind als Komposition stetiger Funktionen stetig, und damit ist insbesondere $ f$ differenzierbar. Es ist

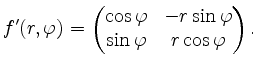
$\displaystyle f'(r,\varphi) = \begin{pmatrix} \cos \varphi & - r \sin \varphi\\ \sin \varphi & r \cos \varphi \end{pmatrix}. $

Die Determinante der Jacobimatrix ergibt sich zu $ \det f'(r,\varphi) = r ((\cos \varphi)^2 + (\sin \varphi)^2) = r$ .

(b)
Es ist

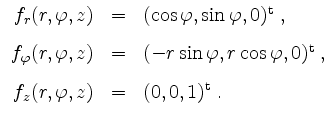
$\displaystyle \begin{array}{rcl} f_r(r,\varphi,z) & = & (\cos \varphi, \sin \va... ...}\; ,\vspace{3mm}\\ f_z(r,\varphi,z) & = & (0,0,1)^\mathrm{t} \; . \end{array}$

Die partiellen Ableitungen sind als Komposition stetiger Funktionen stetig, und daher ist $ f$ differenzierbar ist. Es wird

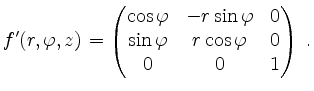
$\displaystyle f'(r,\varphi,z) = \begin{pmatrix} \cos \varphi & - r \sin \varphi & 0\\ \sin \varphi & r \cos \varphi & 0\\ 0 & 0 & 1 \end{pmatrix}\; . $

Mittels Laplace-Entwicklung und Aufgabenteil (a) erhalten wir

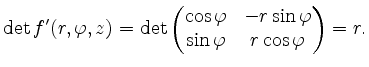
$\displaystyle \det f'(r, \varphi, z) = \det \begin{pmatrix} \cos \varphi & - r \sin \varphi\\ \sin \varphi & r \cos \varphi \end{pmatrix}= r. $

(c)
Die partiellen Ableitungen von $ f$ ergeben sich zu

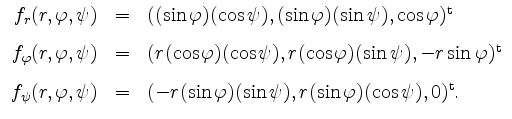
$\displaystyle \begin{array}{rcl} f_r(r,\varphi,\psi) & = & ((\sin\varphi) (\cos... ...\sin\varphi) (\sin\psi), r (\sin\varphi) (\cos\psi), 0)^\mathrm{t}. \end{array}$

Die partiellen Ableitungen sind als Komposition stetiger Funktionen stetig, und demzufolge ist $ f$ differenzierbar mit

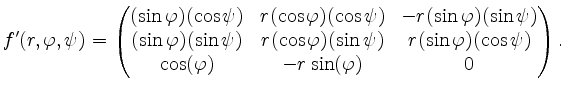
$\displaystyle f'(r,\varphi,\psi) = \begin{pmatrix} (\sin\varphi) (\cos\psi) & ... ...sin\varphi) (\cos\psi)\\ \cos(\varphi) & - r \sin(\varphi) & 0 \end{pmatrix}. $

Wir berechnen die Determinante von $ f'$ mittels Laplace-Entwicklung zu

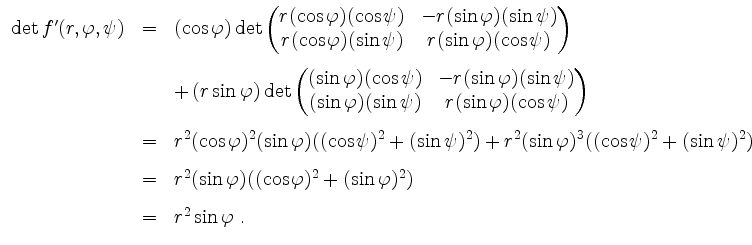
$\displaystyle \begin{array}{rcl} \det f'(r,\varphi,\psi) & = & (\cos\varphi) \d... ...rphi)^2 + (\sin\varphi)^2)\vspace{3mm}\\ & = & r^2 \sin\varphi\; . \end{array}$

2.
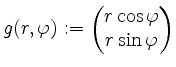Sei $ g(r,\varphi) := \begin{pmatrix}r \cos \varphi\\ r \sin \varphi \end{pmatrix}$ . Wir berechnen die Ableitung von $ F = f \circ g$ mittels Kettenregel und Aufgabenteil 1. (a) zu

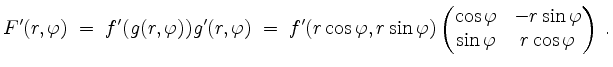
$\displaystyle F'(r,\varphi) \; = \; f'(g(r,\varphi)) g'(r,\varphi) \;=\; f'(r \... ...s \varphi & - r \sin \varphi\\ \sin \varphi & r \cos \varphi \end{pmatrix}\;. $

Diese Gleichung können wir nach $ f'(r \cos \varphi, r \sin \varphi)$ auflösen, indem wir mit der inversen Matrix von rechts multiplizieren. Es wird

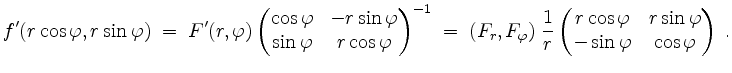
$\displaystyle f'(r \cos \varphi, r \sin \varphi) \;=\; F'(r,\varphi)\begin{pmat... ...pmatrix}r\cos\varphi&r\sin\varphi\\ -\sin\varphi & \cos\varphi\end{pmatrix}\;. $

Daraus ergibt sich

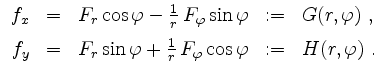
$\displaystyle \begin{array}{rclcl} f_x &=& F_r\cos\varphi -\frac{1}{r}\,F_\varp... ...\sin\varphi +\frac{1}{r}\,F_\varphi\cos\varphi &:=& H(r,\varphi)\;. \end{array}$

Verwendet man dieses Ergebnis für $ f_x$ und $ G$ bzw. $ f_y$ und $ H$ anstelle von $ f$ und $ F$ , so ergibt sich

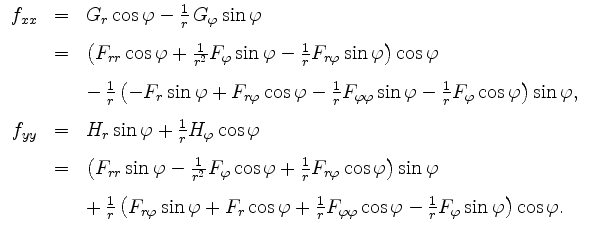
$\displaystyle \begin{array}{rcl} f_{xx} & = & G_r \cos\varphi - \frac{1}{r}\,G_... ...s \varphi - \frac{1}{r} F_\varphi \sin \varphi \right) \cos\varphi. \end{array}$

Es folgt also letztendlich

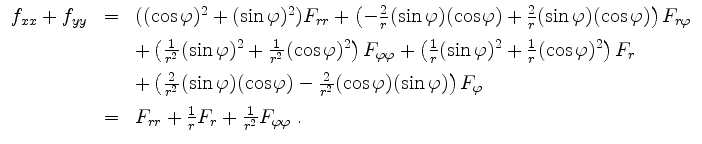
$\displaystyle \begin{array}{rcl} f_{xx} + f_{yy} &=& ((\cos\varphi)^2+(\sin\va... ... &=& F_{rr} + \frac{1}{r} F_r + \frac{1}{r^2} F_{\varphi\varphi}\;. \end{array}$

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006