Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1330: Schwerpunkt von Massepunkten

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Berechnen Sie das globale Minimum der Funktion

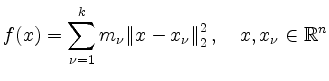
$\displaystyle f(x)=\sum_{\nu=1}^k{m_\nu {\Vert x-x_\nu\Vert}^2_2}\,,\quad x,x_\nu \in\mathbb{R}^n $

für gegebene Punkte $ x_\nu$ und positive Konstanten $ m_\nu$ .

Es ist

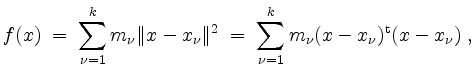
$\displaystyle f(x)\;=\;\sum_{\nu=1}^k{m_\nu \Vert x-x_\nu\Vert^2}\;=\;\sum_{\nu=1}^k{m_\nu(x-x_\nu)^\mathrm{t} (x-x_\nu)}\; , $

und demzufolge

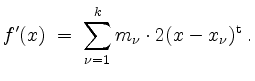
$\displaystyle f'(x)\;=\;\sum_{\nu=1}^k{m_\nu\cdot 2(x-x_\nu)^\mathrm{t}}\; . $

Ferner berechnen wir

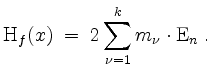
$\displaystyle \mathrm{H}_f(x)\;=\;2\sum_{\nu=1}^k{m_\nu}\cdot \mathrm{E}_n\; . $

Aus der notwendigen Bedingung erhalten wir

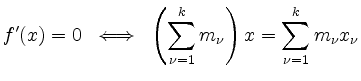
$\displaystyle f'(x)=0 \;\iff\; \left(\sum_{\nu=1}^k{m_\nu}\right)x=\sum_{\nu=1}^k{m_\nu x_\nu} $

und erhalten als einzigen kritischen Punkt

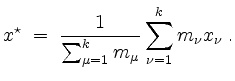
$\displaystyle x^\star\;=\;\frac{1}{\sum_{\mu=1}^k{m_\mu}}\sum_{\nu=1}^k{m_\nu x_\nu}\; . $

Die Hessematrix ist als Diagonalmatrix mit positiven Diagonaleinträgen positiv definit für alle $ x\in\mathbb{R}^n$ , so daß wir aus dem Satz von Taylor ein $ \xi\in\overline{x,x^\star}$ mit

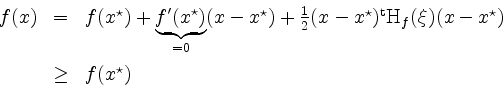
\begin{displaymath} \begin{array}{rcl} f(x) & = & f(x^\star)+\underbrace{f'(x^\s... ...\xi)(x-x^\star)\vspace*{2mm}\\ & \geq & f(x^\star) \end{array}\end{displaymath}

erhalten. Gleichheit tritt genau dann ein, wenn $ x=x^\star$ ist.

Dies zeigt, daß $ f$ bei $ x^\star$ ein globales Minimum annimmt.

Bemerkung. Interpretiert man die Größen $ m_\nu$ als Massen von Massenpunkten an den Orten $ x_\nu$ , so befindet sich das globale Minimum in deren Schwerpunkt $ x^\star$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006