
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1331: Extrema auf der abgeschlossenen Kreisscheibe |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
auf der Einheitskreisscheibe
Zunächst untersuchen wir die Funktion auf lokale Extrema auf der offenen
Menge
![]() .
.
Die notwendige Bedingung
liefert
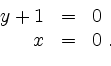
Der einzige kritische Punkt ist somit der Punkt
Also gibt es auf
![]() kein lokales Extremum. Eine globale Extremstelle auf der gesamten Menge
kein lokales Extremum. Eine globale Extremstelle auf der gesamten Menge
![]() , welche in
, welche in
![]() liegt, wäre aber insbesondere eine solche lokale
Extremstelle. Damit gibt es auf
liegt, wäre aber insbesondere eine solche lokale
Extremstelle. Damit gibt es auf
![]() auch kein globales Extremum.
auch kein globales Extremum.
Da die Menge
![]() kompakt ist, und da
kompakt ist, und da ![]() stetig ist, existieren dort sowohl globales Maximum als
auch globales Minimum. Nach dem obigen Resultat werden beide auf dem Rand
stetig ist, existieren dort sowohl globales Maximum als
auch globales Minimum. Nach dem obigen Resultat werden beide auf dem Rand
![]() angenommen.
angenommen.
Die Nebenbedingung lautet mit
![]() also
also
![]() . Sei
. Sei
Wir wollen die Multiplikatorenregel von Lagrange verwenden. Die dabei notwendige Voraussetzung
ist erfüllt für alle
Wir bestimmen nun alle regulären kritischen Punkte unter Nebenbedingung ![]() vermittels
vermittels
d.h. vermittels
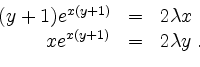
Im Falle ![]() folgt aus der Nebenbedingung
folgt aus der Nebenbedingung ![]() , und somit
, und somit
![]() . Nun gibt
. Nun gibt ![]() einen Widerspruch.
Dagegen ist
einen Widerspruch.
Dagegen ist
![]() in der Tat ein kritischer Punkt.
in der Tat ein kritischer Punkt.
Im Falle ![]() ist gemäß der Nebenbedingung
ist gemäß der Nebenbedingung ![]() , im Widerspruch zur obigen Gleichung.
, im Widerspruch zur obigen Gleichung.
Daher können wir uns von nun an auf den Fall ![]() und
und ![]() konzentrieren. Es ergibt sich
konzentrieren. Es ergibt sich
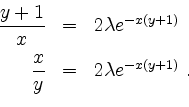
Gleichsetzen der linken Seiten gibt
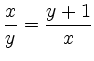 , d.h.
, d.h.
und hieraus
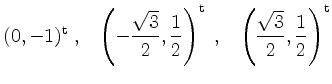
für lokale Extremstellen unter der Nebenbedingung
Wir vergleichen die Funktionswerte
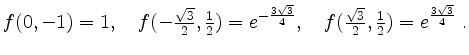
Also hat
Wie bereits oben ausgeführt, sind dies auch die globalen Extrema von ![]() auf der Menge
auf der Menge
![]() .
.
Untersuchen wir unsere kritischen Punkte interessehalber auch noch auf lokale Extrema unter Nebenbedingung ![]() . Natürlich wissen wir bereits,
daß die beiden globalen Extrema auch lokale Extrema zu sein haben. Mit etwas Glück - unsere diesbezügliche Bedingung ist zwar hinreichend, nicht
aber notwendig - sollte sich das auch bestätigen.
. Natürlich wissen wir bereits,
daß die beiden globalen Extrema auch lokale Extrema zu sein haben. Mit etwas Glück - unsere diesbezügliche Bedingung ist zwar hinreichend, nicht
aber notwendig - sollte sich das auch bestätigen.
Für beliebiges ![]() und beliebiges
und beliebiges ![]() wird
wird
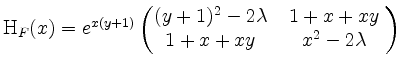 .
.
Bei
![]() ist
ist
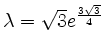 , es ist
, es ist
![]() , und wir können
, und wir können
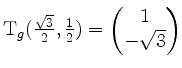 nehmen.
Die relative Hessematrix ergibt sich zu
nehmen.
Die relative Hessematrix ergibt sich zu
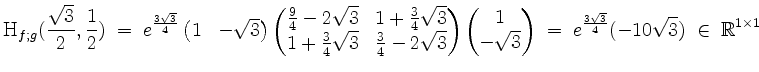
und ist negativ definit. In der Tat liegt also bei
Bei
![]() ist
ist
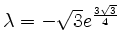 , es ist
, es ist
![]() , und wir können
, und wir können
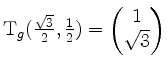 nehmen.
Die relative Hessematrix ergibt sich zu
nehmen.
Die relative Hessematrix ergibt sich zu
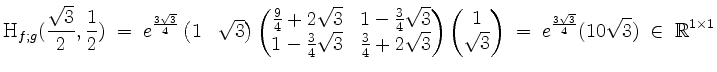
und ist positiv definit. In der Tat liegt also bei
Bei ![]() ist
ist
![]() , es ist
, es ist
![]() , und wir können
, und wir können
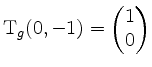 nehmen.
Die relative Hessematrix ergibt sich zu
nehmen.
Die relative Hessematrix ergibt sich zu
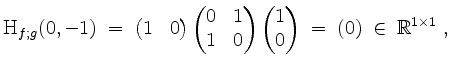
und wir können im einzigen noch offengebliebenen Fall keine Entscheidung über ein lokales Extremum unter Nebenbedingung
Skizze von ![]() auf
auf
![]() .
.
![\includegraphics[width = 8cm]{s3.eps}](/inhalt/loesung/loesung684/img53.png)
| automatisch erstellt am 11. 8. 2006 |