Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1333: Extrema mit Nebenbedingungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

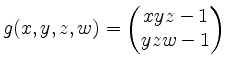Sei $ f(x,y,z,w) := x^2 + y^2 + z^2 + w^2$ , und sei $ g(x,y,z,w) = \begin{pmatrix}xyz - 1 \\ yzw - 1\end{pmatrix}$ , beides definiert auf $ P := \{ (x,y,z,w)^\mathrm{t}\in\mathbb{R}^4\; \vert\; x > 0,\; y > 0,\; z > 0,\; w > 0\}$ .

1.
Bestimme die lokalen Extrema von $ f$ unter der Nebenbedingung $ g = 0$ vermittels der Lagrangeschen Multiplikatorenmethode.
2.
Bestimme die lokalen Extrema von $ f$ unter der Nebenbedingung $ g = 0$ , indem zunächst in $ f$ die von der Bedingung $ g = 0$ herrührenden Substitutionen $ x = w = (yz)^{-1}$ vorgenommen werden, und die resultierende Funktion in Abhängigkeit von den Variablen $ y$ und $ z$ auf lokale Extrema untersucht wird.

1.
Mit $ F := f - \lambda g$ und $ \lambda = (\lambda_1,\lambda_2)$ erhalten wir

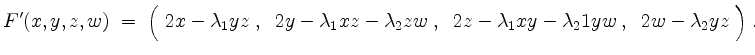
$\displaystyle F'(x,y,z,w) \;=\; \Big(\; 2x - \lambda_1 yz\; ,\;\; 2y - \lambda_... ... \;\; 2z - \lambda_1 xy - \lambda_21 yw\; , \;\; 2w - \lambda_2 yz\;\Big)\; . $

Zusammen mit $ g = 0$ liefert dies das Gleichungssystem

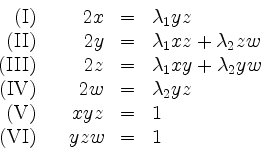
\begin{displaymath} \begin{array}{rcrcl} \mathrm{(I)} & & 2x & = & \lambda_1 yz ... ...& xyz & = & 1 \\ \mathrm{(VI)} & & yzw & = & 1 \\ \end{array}\end{displaymath}

zur Ermittlung der kritischen Punkte.

Aus (V, VI) folgt, daß $ x = w$ .

Aus (I, IV) ergeben sich $ \lambda_1 = \lambda_2 = \frac{2x}{yz}$ .

Aus (II, III) erhalten wir $ y^2 = z^2 = 2x^2$ , und also wegen $ (x,y,z,w)^\mathrm{t}\in P$ auch $ y = z = 2^{1/2}x$ .

Aus (V) folgt schließlich $ x = 2^{-1/3}$ , und wir erhalten den kritischen Punkt

$\displaystyle (2^{-1/3},2^{1/6},2^{1/6},2^{-1/3})^\mathrm{t}\; . $

Da

\begin{displaymath} g'(x,y,z,w) \;=\; \left[ \begin{array}{cccc} yz & xz & xy & 0 \\ 0 & zw & yw & yz \\ \end{array}\right] \end{displaymath}

auf ganz $ P$ Rang $ 2$ hat, ist der gefundene kritische Punkt regulär.

Da insbesondere

\begin{displaymath} g'(2^{-1/3},2^{1/6},2^{1/6},2^{-1/3}) \;=\; \left[ \begin{a... ... 0 & 2^{-1/6} & 2^{-1/6} & 2^{1/3} \\ \end{array}\right]\; , \end{displaymath}

können wir z.B.

\begin{displaymath} \mathrm{T}_g(2^{-1/3},2^{1/6},2^{1/6},2^{-1/3}) \;=\; \left... ...1 & 0 \\ 0 & 1 \\ 0 & -1 \\ -1 & 0 \\ \end{array}\right] \end{displaymath}

wählen.

Allgemein ist

\begin{displaymath} \mathrm{H}_F(x,y,z,w) \;=\; \left[ \begin{array}{cccc} 2 & ... ...0 & -\lambda_2 z & -\lambda_2 y & 2 \\ \end{array}\right]\; . \end{displaymath}

Speziell wird die relative Hessematrix am kritischen Punkt also zu

\begin{displaymath} \begin{array}{rcl} \mathrm{H}_{f;g}(2^{-1/3},2^{1/6},2^{1/6}... ...y}{rr} 4 & 0 \\ 0 & 8 \\ \end{array}\right]\; , \end{array}\end{displaymath}

und ist somit positiv definit. Mithin liegt bei $ (2^{-1/3},2^{1/6},2^{1/6},2^{-1/3})^\mathrm{t} \approx (0.7937,1.122,1.122,0.7937)^\mathrm{t}$ ein lokales Minimum unter Nebenbedingung $ g = 0$ vor.

2.
Substitution von $ x = w = \frac{1}{yz}$ in $ f$ liefert die Funktion

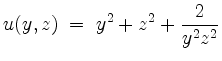
$\displaystyle u(y,z) \;=\; y^2 + z^2 + \frac{2}{y^2 z^2} $

auf $ \tilde{P} := \{ (y,z)^\mathrm{t}\in\mathbb{R}^2 \; \vert\; y > 0,\; z > 0\}$ .

Die Ableitung

$\displaystyle u'(y,z) \;=\; (2y - 4z^{-2}y^{-3},\; 2z - 4y^{-2}z^{-3}) $

verschwindet auf $ \tilde{P}$ gerade bei $ z = y = 2^{1/6}$ .

Allgemein ist

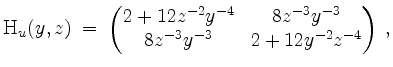
$\displaystyle \mathrm{H}_u(y,z) \;=\; \begin{pmatrix}2 + 12 z^{-2} y^{-4} & 8z^{-3}y^{-3}\\ 8z^{-3}y^{-3} & 2 + 12 y^{-2} z^{-4}\end{pmatrix} \; , $

so daß sich im kritischen Punkt $ (2^{1/6},2^{1/6})$ die positiv definite Hessematrix

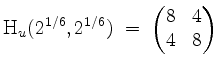
$\displaystyle \mathrm{H}_u(2^{1/6},2^{1/6}) \;=\; \begin{pmatrix}8&4\\ 4&8\end{pmatrix} $

ergibt. Somit liegt bei $ (2^{1/6},2^{1/6})$ ein lokales Minimum vor, in Übereinstimmung mit (1).

Man beachte, daß der zweite Lösungsweg nur gangbar ist, da sich in den Nebenbedingungen Variablen rechnerisch isolieren lassen.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006