Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1335: Hessematrix einer impliziten Funktion und Gültigkeit einer partiellen Differentialgleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Gegeben sei die Funktion

$\displaystyle f(x_1,x_2,y)=x_1 x_2+(1+x_2)y + y^3\,. $

a)
Zeigen Sie, dass $ f(x_1,x_2,y)=0$ im Punkt $ (0,0,0)$ lokal nach $ y=g(x_1,x_2)$ auflösbar ist.
b)
Zeigen Sie, dass $ g$ zweimal stetig differenzierbar ist. Bestimmen Sie $ g'(0,0)$ und die Hessematrix $ H_g(0,0)$ .
c)
Zeigen Sie, dass $ g$ der partiellen Differentialgleichung $ (1+6gg_{x_2})g_{x_1}+(1+x_2+3g^2)g_{x_1x_2}=0$ genügt.

1.
Sei $ f:\mathbb{R}^3\to\mathbb{R}$ definiert durch $ f(x_1,x_2,y):=x_1x_2+(1+x_2)y+y^3$ . Dann ist $ f$ stetig differenzierbar, und es folgt

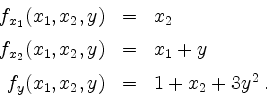
\begin{displaymath} \begin{array}{rcl} f_{x_1}(x_1,x_2,y) &=& x_2\vspace*{2mm}\\... ...+y\vspace*{2mm}\\ f_y(x_1,x_2,y) &=& 1+x_2+3y^2\;. \end{array}\end{displaymath}

Speziell ist

$\displaystyle f_y(0,0,0) \;=\; 1\ne 0\;. $

Nach dem Satz über implizite Funktionen ist daher die Gleichung $ f(x_1,x_2,y)=0$ lokal um den Punkt $ (0,0,0)^\mathrm{t}$ nach $ y$ auflösbar.
2.
Nach 1. gibt es also Umgebungen $ U\subseteq\mathbb{R}^2$ von $ (0,0)^\mathrm{t}$ und $ V\subseteq\mathbb{R}$ von 0 sowie (genau) eine stetig differenzierbare Funktion $ g:U\to V$ so, daß Mit der Bezeichnung $ x=(x_1,x_2)^\mathrm{t}$ wird

$\displaystyle g'(x) \;=\; -f_y(x,g(x))^{-1} f_x(x,g(x)) \;=\; (1+x_2+3y^2)^{-1} (x_2,x_1 + y) \; . $

Speziell ist $ g$ zweimal stetig differenzierbar - beachte, daß $ f_y(x,g(x))$ für $ x\in U_0$ nicht verschwindet.

Insbesondere wird

$\displaystyle g'(0) \;=\; (0,0) $

wegen $ y = 0$ dort.

Eine weitere Anwendung der Kettenregel ergibt

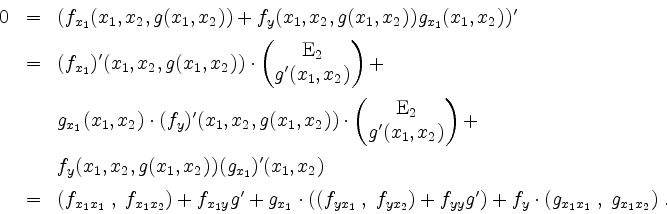
\begin{displaymath} \begin{array}{rcl} 0 &=& (f_{x_1}(x_1,x_2,g(x_1,x_2))+f_y(x_... ...})+f_{yy}g')+f_y\cdot(g_{x_1x_1}\;,\;g_{x_1x_2})\;. \end{array}\end{displaymath}

Analog erhält man

$\displaystyle 0 \;=\; (f_{x_2x_1}\;,\;f_{x_2x_2})+f_{x_2y}g'+g_{x_2}\cdot((f_{y x_1}\;,\;f_{y x_2})+f_{yy}g') +f_y\cdot(g_{x_2x_1}\;,\;g_{x_2x_2})\;. $

Setzt man speziell den Punkt $ (x_1,x_2)^\mathrm{t}=(0,0)^\mathrm{t}$ ein, so erhält man

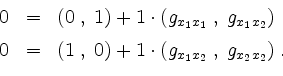
\begin{displaymath} \begin{array}{rcl} 0 &=& (0\;,\; 1)+1\cdot(g_{x_1x_1}\;,\;g_... ...&=& (1\;,\; 0)+1\cdot(g_{x_1x_2}\;,\;g_{x_2x_2})\;. \end{array}\end{displaymath}

Insgesamt ergibt sich

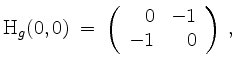
$\displaystyle \mathrm{H}_g(0,0) \;=\; \left(\begin{array}{rr}0&-1\\ -1&0\end{array}\right) \; , $

und diese Matrix hat Signatur $ (1,1)$ , da sie einen positiven und einen negativen Eigenwert besitzt, wie uns z.B. der beidseitige Gaußalgorithmus liefert. Also liegt hat $ g(x_1,x_2)$ bei $ (0,0)^\mathrm{t}$ einen Sattelpunkt.

3.
Obiges liefert unter anderem

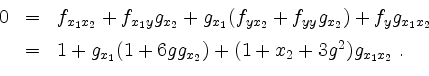
\begin{displaymath} \begin{array}{rcl} 0 &=& f_{x_1x_2} +f_{x_1 y}g_{x_2} + g_{... ...=& 1+g_{x_1}(1+6gg_{x_2})+(1+x_2+3g^2)g_{x_1x_2}\;. \end{array}\end{displaymath}

Hier eine Skizze der Lösungsmenge von $ f(x_1,x_2,y)=0$ . Man erkennt einen Sattelpunkt bei $ (0,0)^\mathrm{t}$ .

\includegraphics[width = 12cm]{s2.eps}
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006