
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1339: Konservative Vektorfelder |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Für welche Werte von ![]() erfüllt das Vektorfeld
erfüllt das Vektorfeld
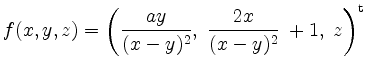 die Integrabilitätsbedingungen?
die Integrabilitätsbedingungen?
Bestimme einen maximalen Definitionsbereich, auf dem ![]() konservativ ist, und dort eine Stammfunktion.
konservativ ist, und dort eine Stammfunktion.
Es wird
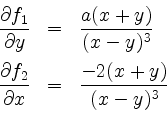
und
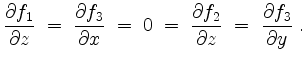
Also erfüllt ![]() genau dann die Integrabilitätsbedingungen, wenn
genau dann die Integrabilitätsbedingungen, wenn ![]() .
.
Man kann eine Stammfunktion ![]() in diesem Falle wie folgt berechnen.
in diesem Falle wie folgt berechnen.
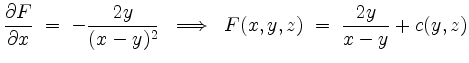
für eine Funktion
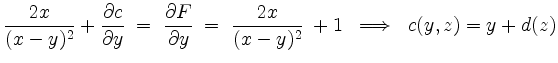
für eine Funktion
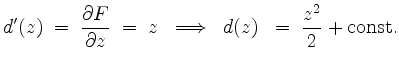
Wir können also
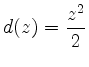 wählen und erhalten als Stammfunktion
wählen und erhalten als Stammfunktion
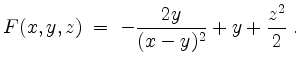
Der maximale Definitionsbereich ist dabei
| automatisch erstellt am 11. 8. 2006 |