Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1341: Volumen der n-dimensionalen Kugel

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei $ n\in\mathbb{Z}_{\ge 1}$ , und sei $ r \ge 0$ .

Sei $ K_n(r)=\{(x_1,\dots,x_n)^\mathrm{t}\in\mathbb{R}^n\ \vert\ x_1^2+\dots+x_n^2\leq r^2\}$ eine $ n-$ dimensionale Kugel mit Radius $ r$ .

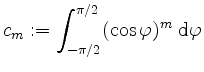Wir setzen $ c_m:=\displaystyle\int_{-\pi/2}^{\pi/2}(\cos\varphi)^m\; \mathrm{d}\varphi$ für $ m\in\mathbb{Z}_{\ge 1}$ .

Zeige.

  1. Es gilt $ \mathrm{vol}(K_n(r))=r^nc_1\cdot\dots\cdot c_n$ .

  2. Es gilt für $ n\geq 2$ die Rekursionsgleichung $ n c_n = (n-1) c_{n-2}$ .

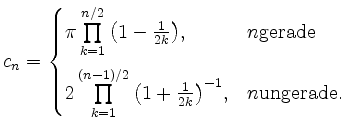  3. Es gilt $ c_n =\begin{cases} \par \pi\prod\limits_{k=1}^{n/2}{\left(1-\frac{1}{2k}\right... ...{(n-1)/2}{\left(1+\frac{1}{2k}\right)^{-1}}, & n\mathrm{ ungerade.} \end{cases}$ .

  4. Für $ m\in\mathbb{Z}_{\ge 1}$ gelten die Volumenformeln

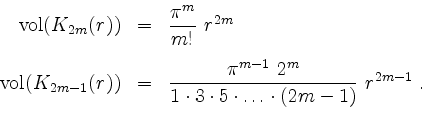
    \begin{displaymath} \begin{array}{rcl} \mathrm{vol}(K_{2m}(r)) & = & \dfrac{\pi^... ...\cdot 3\cdot 5\cdot\ldots\cdot (2m-1)}\ r^{2m-1}\ . \end{array}\end{displaymath}

  1. $ n=1:$
    Es ist

    $\displaystyle K_1(r)=\{x_1\in\mathbb{R}\ \vert\ x_1^2\leq r^2\}=[-r,r], $

    also folgt

    $\displaystyle \mathrm{vol}(K_1(r))=2r=r^1c_1, $

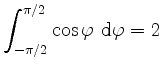    da $ \displaystyle\int_{-\pi/2}^{\pi/2}{\cos\varphi\ \mathrm{d}\varphi}=2$ gilt.
    $ n\to n+1:$
    Für $ x_{n+1}\in\mathbb{R}$ und $ M = K_{n+1}(r)$ sind

    $\displaystyle M_{x_{n+1}}=\{(x_1,\dots,x_n)^\mathrm{t}\in\mathbb{R}^n\; \vert\;... ...2-x_{n+1}^2}\right) & \mathrm{f''ur } x_{n+1}\in [-r,r] \\ \end{array}\right. $

    und

    $\displaystyle M' \; =\; \{x_{n+1}\in\mathbb{R}\; \vert\; M_{x_{n+1}}\neq\emptyset\} \; =\; [-r,r] $

    meßbar, und es folgt

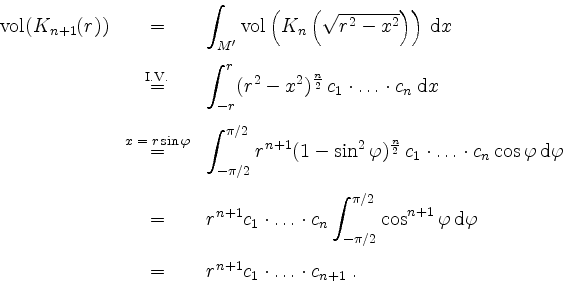
    \begin{displaymath} \begin{array}{rcl} \mathrm{vol}(K_{n+1}(r)) & = & \display... ...}\\ & = & r^{n+1}c_1\cdot\ldots\cdot c_{n+1} \; . \end{array}\end{displaymath}

  2. Für $ n\geq 2$ gilt

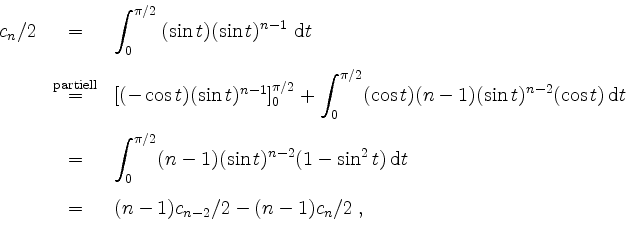
    \begin{displaymath} \begin{array}{rcl} c_n/2 & = & \displaystyle\int_0^{\pi/2}{... ...e{3mm}\\ & = & (n-1)c_{n-2}/2 - (n-1)c_n/2 \;, \\ \end{array}\end{displaymath}

    und also

    $\displaystyle n c_n \;=\; (n-1)c_{n-2}\; . $

  3. Für $ n\geq 1$ folgt

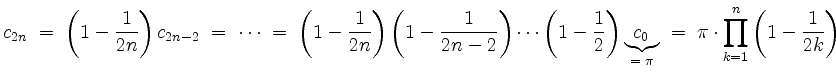
    $\displaystyle c_{2n}\; =\; \left(1-\frac{1}{2n}\right)c_{2n-2} \; =\; \cdots \;... ...brace{c_0}_{=\; \pi} \; =\; \pi\cdot\prod_{k=1}^n{\left(1-\frac{1}{2k}\right)} $

    sowie

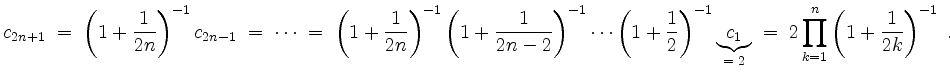
    $\displaystyle c_{2n+1} \; =\; \left(1+\frac{1}{2n}\right)^{-1} c_{2n-1} \; =\; ... ...erbrace{c_1}_{=\; 2} \; =\; 2\prod_{k=1}^n \left(1+\frac{1}{2k}\right)^{-1}\ . $

    Somit gilt

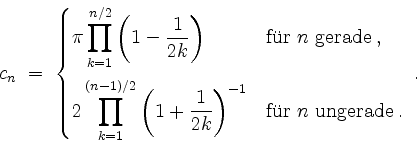
    \begin{displaymath} c_n \;=\; \begin{cases} \pi\displaystyle\prod\limits_{k=1}^... ...right)^{-1}} & \mbox{f''ur $n$\ ungerade}\; . \end{cases} \; . \end{displaymath}

  4. Wir müssen zeigen, daß

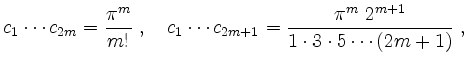
    $\displaystyle c_1\cdots c_{2m}=\frac{\pi^m}{m!}\; ,\quad c_1\cdots c_{2m+1}=\frac{\pi^m\ 2^{m+1}}{1\cdot 3\cdot 5\cdots (2m+1)}\; , $

    zeigen wir dies per Induktion für $ m\ge 0$ .

    $ m=0:$
    Für die erste Formel ist nichts zu zeigen. Für die zweite ergibt sich

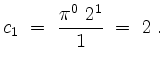
    $\displaystyle c_1\;=\; \frac{\pi^0\ 2^1}{1}\;=\;2 \; . $

    $ m\to m+1:$
    Wir folgern

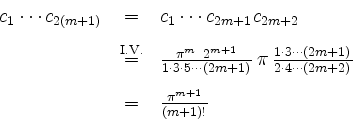
    \begin{displaymath} \begin{array}{rcl} c_1\cdots c_{2(m+1)} &=& c_1\cdots c_{2m... ...(2m+2)}\vspace{3mm}\\ &=& \frac{\pi^{m+1}}{(m+1)!} \end{array}\end{displaymath}

    sowie

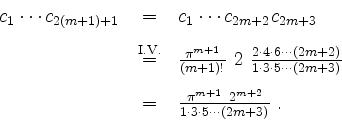
    \begin{displaymath} \begin{array}{rcl} c_1\cdots c_{2(m+1)+1} &=& c_1\cdots c_{2... ...i^{m+1}\ 2^{m+2}}{1\cdot 3\cdot 5\cdots (2m+3)}\; . \end{array}\end{displaymath}

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006