Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Hinweis zu

Aufgabe 1345: Gaußsches Fehlerintegral

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Für $ a,\, \rho \,\geq\, 0$ seien

$\displaystyle K_\rho \; := \; \{ (x,y)^\mathrm{t} \in \mathbb{R}^2 \; \vert\; x^2 + y^2 \leq \rho^2 \mathrm{ mit } x,y \geq 0 \} \;, $

und

$\displaystyle Q_a \; :=\; \{ (x,y)^\mathrm{t} \in \mathbb{R}^2 \; \vert\; 0 \leq x \leq a, \; 0 \leq y \leq a\} \; , $

definiert.

Zeige, daß die Gleichungen

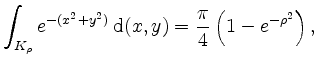
$\displaystyle \displaystyle \int_{K_\rho} e^{-(x^2+y^2)} \, \mathrm{d}(x,y) = \dfrac{\pi}{4} \left( 1 - e^{-\rho^2} \right), $

und

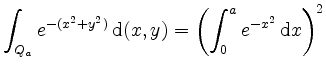
$\displaystyle \displaystyle \int_{Q_a} e^{-(x^2+y^2)} \, \mathrm{d}(x,y) = \left( \int_0^a e^{-x^2} \, \mathrm{d} x \right)^2 $

gelten.

Zeige damit die Identität des Gaußschen Fehlerintegrals

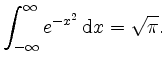
$\displaystyle \displaystyle \int_{-\infty}^\infty e^{-x^2} \, \mathrm{d} x = \sqrt{\pi}. $

Benutze die Polarkoordinatentransformation, bzw. den Satz von Fubini, um die ersten beiden Aussagen zu zeigen.

Zur Frage des Gaußschen Fehlerintegrals argumentiere schließlich wie folgt. Mit $ a$ gehen auch der Radius der größten in $ Q_a$ enthaltenen Viertelkreises $ K_{\rho_1}$ und der Radius des kleinsten $ Q_a$ enthaltenden Viertelkreises $ K_{\rho_2}$ gegen $ \infty$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006