
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1345: Gaußsches Fehlerintegral |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Für
![]() seien
seien
Zeige, daß die Gleichungen
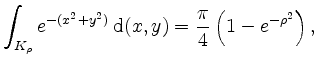
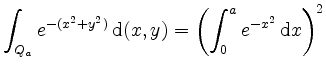
Zeige damit die Identität des Gaußschen Fehlerintegrals
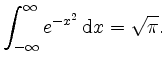
Verwenden wir die Polarkoordinatentransformation
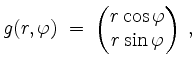
so ist
Mittels der Substitutionsregel errechnen wir
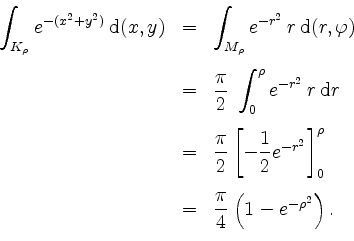
Der Satz von Fubini liefert
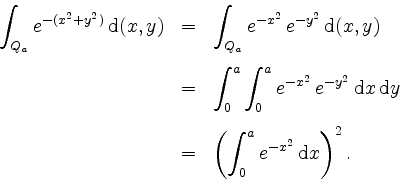
Es ist
für alle
![\includegraphics[width = 4cm]{s3.eps}](/inhalt/loesung/loesung712/img9.png)
Da wir über eine nichtnegative Funktion integrieren, erhalten wir den Zusammenhang
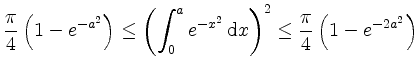
für alle
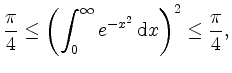
d.h.
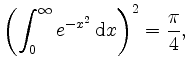
und somit
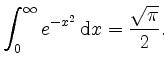
Nutzen wir nun die Symmetrie der Funktion
![]() bezüglich der
bezüglich der ![]() -Achse aus, so erhalten
wir die Behauptung,
-Achse aus, so erhalten
wir die Behauptung,
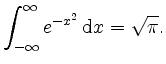
| automatisch erstellt am 11. 8. 2006 |