Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 1346: Oberfläche des Torus und des hyperbolischen Paraboloids

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 1346: Oberfläche des Torus und des hyperbolischen Paraboloids

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei .

(i)

Berechne die Oberfläche des Torus

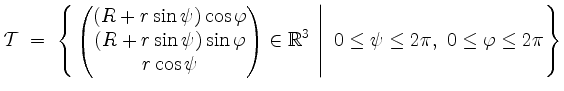
$\displaystyle \mathcal T \; =\; \left\{\left.\begin{pmatrix}(R+r\sin\psi)\cos\v... ...\mathbb{R}^3\ \right\vert\ 0\leq\psi\leq 2\pi,\ 0\leq\varphi\leq 2\pi\right\}$

einmal direkt und einmal mittels der zweiten Guldinschen Regel.

(ii)

Berechne die Oberfläche des hyperbolischen Paraboloids

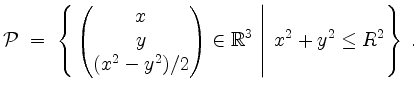
$\displaystyle \mathcal P\; =\;\left\{\left.\begin{pmatrix}x\\ y\\ (x^2 - y^2)/2\end{pmatrix}\in\mathbb{R}^3\;\right\vert\; x^2+y^2\leq R^2\right\}\; .$

(i)

$\includegraphics[width=10cm]{torus.eps}$

Lösung mit direkter Rechnung.

Wir schreiben

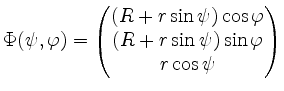
$\displaystyle \Phi(\psi,\varphi) = \begin{pmatrix}(R+r\sin\psi)\cos\varphi\\ (R+r\sin\psi)\sin\varphi\\ r\cos\psi\end{pmatrix}$

mit $\psi,\varphi\in [0,2\pi]$ . Dann sind

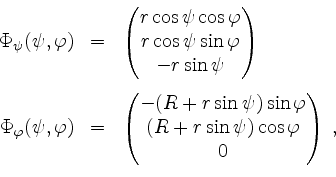
$\begin{displaymath} \begin{array}{rcl} \Phi_\psi(\psi,\varphi) &=& \begin{pmatri... ... (R+r\sin\psi)\cos\varphi\\ 0\end{pmatrix} \; , \\ \end{array}\end{displaymath}$

und folglich

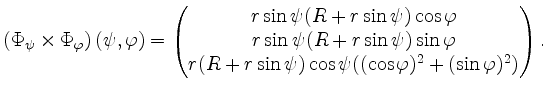
$\displaystyle \left(\Phi_\psi\times \Phi_\varphi\right)(\psi,\varphi)=\begin{pm... ...varphi\\ r(R+r\sin\psi)\cos\psi((\cos\varphi)^2+(\sin\varphi)^2)\end{pmatrix}.$

Wir erhalten

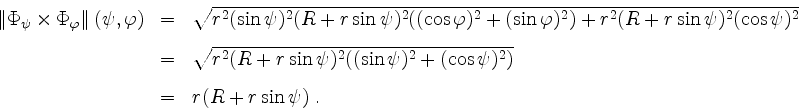
$\begin{displaymath} \begin{array}{rcl} \left\Vert\Phi_\psi\times \Phi_\varphi\ri... ...si)^2)}\vspace{3mm}\\ & = & r(R+r\sin\psi) \; .\\ \end{array}\end{displaymath}$

Damit folgt

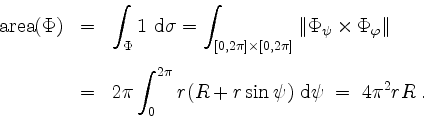
$\begin{displaymath} \begin{array}{rcl} \mathrm{area}(\Phi) &=& \displaystyle\int... ...R+r\sin\psi)\ \mathrm{d}\psi \; =\; 4\pi^2 r R \; . \end{array}\end{displaymath}$

Lösung mit der zweiten Guldinschen Regel.

Wir lassen die in der - -Ebene liegende Kurve $\gamma:[0,2\pi] \to \mathbb{R}^2, \, \varphi \mapsto (R + r \cos\varphi, r \sin \varphi)^\mathrm{t}$ um die -Achse rotieren.

Da es sich bei dieser Kurve $\gamma$ um einen Kreis handelt, ist der Kurvenschwerpunkt der Mittelpunkt dieses Kreises, d.h. $(s_1,s_2)^\mathrm{t} = \left(R,0\right)^\mathrm{t}$ .

Die Länge der Kurve beträgt

$\displaystyle \ell(\gamma) = 2 \pi r \, .$

Nach der zweiten Guldinschen Regel ist der Flächeninhalt des so entstehenden Rotationskörpers, d.h. der Flächeninhalt des Torus, gleich

$\displaystyle \mathrm{area}(\Phi) = \ell(\gamma) \cdot 2\pi s_1 = 4 \pi^2 rR \, .$

(ii)

$\includegraphics[width=10cm]{paraboloid.eps}$

Wir definieren die Fläche

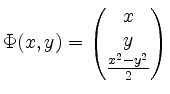
$\displaystyle \Phi(x,y) = \begin{pmatrix}x\\ y\\ \frac{x^2-y^2}{2}\end{pmatrix}$

auf der kompakten Menge 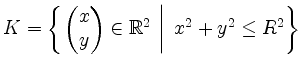$K=\left\{\left.\begin{pmatrix}x\\ y\end{pmatrix}\in\mathbb{R}^2\ \right\vert\ x^2+y^2\leq R^2\right\}$ . Dann ist $\Phi(K)=\mathcal P$ . Wir berechnen

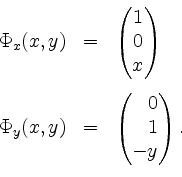
$\begin{displaymath} \begin{array}{rcl} \Phi_x(x,y) &=& \begin{pmatrix}1\\ 0\\ x\... ...egin{pmatrix}\hfill 0\\ \hfill 1\\ -y\end{pmatrix}. \end{array}\end{displaymath}$

Somit ist

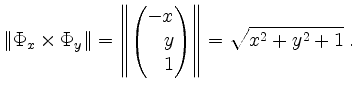
$\displaystyle \Vert\Phi_x\times\Phi_y\Vert=\left\Vert\begin{pmatrix}-x\\ \hfill y\\ \hfill 1\end{pmatrix}\right\Vert=\sqrt{x^2+y^2+1}\; .$

Wir erhalten mit der Polarkoordinatentransformation

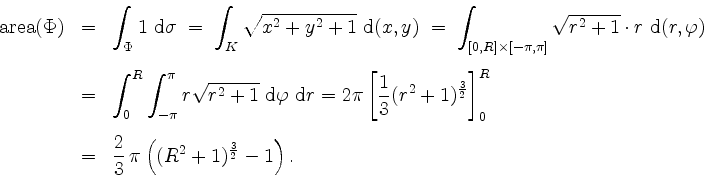
$\begin{displaymath} \begin{array}{rcl} \mathrm{area}(\Phi) &=& \displaystyle\int... ...rac{2}{3}\,\pi\left((R^2+1)^{\frac{3}{2}}-1\right). \end{array}\end{displaymath}$

(Autoren: Künzer/Martin/Tentler/Wahrheit)

[Zurück zur Aufgabe]

automatisch erstellt am 11. 8. 2006