Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Hinweis zu

Aufgabe 1348: Greenscher Integralsatz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Es sei $ S:=\{(x,y)^\mathrm{t} \in \mathbb{R}^2 \,\vert\,x^2+y^2\leq 1\}\ $ , und $ \partial S$ bezeichne den positiv orientierten Rand von $ S$ .

Berechne sowohl direkt als auch über den Greenschen Integralsatz

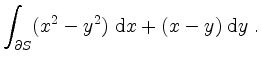
$\displaystyle \int_{\partial S}(x^2-y^2)\;\mathrm{d}x+(x-y)\;\mathrm{d}y\;. $

Für beide Lösungswege empfiehlt sich eine Polarkoordinatentransformation.

Bei der direkten Rechnung sind dann die meisten Summanden des Integranden im Kurvenintegral ungerade Funktionen. Eine Symmetrieüberlegung läßt sie verschwinden.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006