Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 1348: Greenscher Integralsatz

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 1348: Greenscher Integralsatz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Es sei $S:=\{(x,y)^\mathrm{t} \in \mathbb{R}^2 \,\vert\,x^2+y^2\leq 1\}\$ , und $\partial S$ bezeichne den positiv orientierten Rand von .

Berechne sowohl direkt als auch über den Greenschen Integralsatz

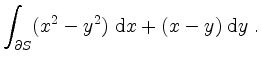
$\displaystyle \int_{\partial S}(x^2-y^2)\;\mathrm{d}x+(x-y)\;\mathrm{d}y\;.$

Mit dem Greenschen Integralsatz und Polarkoordinatentransformation erhalten wir sofort

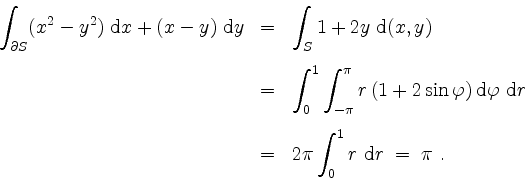
$\begin{displaymath} \begin{array}{rcl} \displaystyle\int_{\partial S}(x^2-y^2)\;... ...splaystyle 2\pi\int_0^1 r\ \mathrm{d}r \;=\; \pi\ . \end{array}\end{displaymath}$

Um direkt rechnen zu können, parametrisieren wir $\partial S=\left\{(x,y)^\mathrm{t}\in\mathbb{R}^2\vert\;x^2+y^2=1\right\}$ durch

$\displaystyle [-\pi,\pi]\to\mathbb{R}^2,\; \varphi\mapsto \begin{pmatrix}\cos\varphi\\ \sin\varphi\end{pmatrix}\;,$

und berechnen das Kurvenintegral

$\begin{displaymath} \begin{array}{rcl} \displaystyle\int_{\partial S}(x^2-y^2)\;... ...phi)\right]_{-\pi}^\pi\vspace{3mm}\\ & = & \pi\; . \end{array}\end{displaymath}$

(Autoren: Künzer/Martin/Tentler/Wahrheit)

[Zurück zur Aufgabe]

automatisch erstellt am 11. 8. 2006