Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1349: Schwerpunkt einer regulären Menge

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

  1. Sei $ B\subseteq\mathbb{R}^2$ ein regulärer Bereich mit positiv orientierter Randkurve $ \gamma:[a,b]\to\mathbb{R}^2$ , und es gelte $ \mathrm{vol}(B)>0$ .

    Zeige, daß für den Schwerpunkt $ (x_S,y_S)^\mathrm{t}$ von $ B$ gilt

    \begin{displaymath} \begin{array}{rcl} x_S & = & -\dfrac{1}{\mathrm{vol}(B)}\dis... ...vol}(B)}\displaystyle\int_\gamma xy\;\mathrm{d}y\;. \end{array}\end{displaymath}

  2. Es sei $ B\subseteq\mathbb{R}^2$ der Bereich im 1. Quadranten, der von den Geraden $ y=x$ , $ y=1/x$ und $ y=x/4$ begrenzt wird. Bestimme mit Hilfe des Greenschen Integralsatzes den Inhalt von $ B$ . Bestimme ferner den Schwerpunkt von $ B$ .

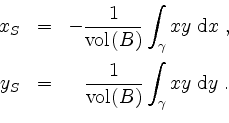
    Skizze der Berandungskurven.

    \includegraphics[width = 8cm]{p3.eps}

  1. Der Greensche Integralsatz liefert zum einen

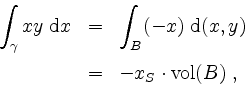
    \begin{displaymath} \begin{array}{rcl} \displaystyle\int_\gamma xy\;\mathrm{d}x ... ...ce*{2mm}\\ & = & -x_S\cdot\mathrm{vol}(B) \; , \\ \end{array}\end{displaymath}

    und zum anderen

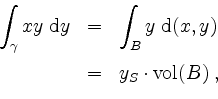
    \begin{displaymath} \begin{array}{rcl} \displaystyle\int_\gamma xy\;\mathrm{d}y ... ...ace*{2mm}\\ & = & y_S\cdot\mathrm{vol}(B) \; , \\ \end{array}\end{displaymath}

    wie behauptet.

  2. Skizze des Bereichs $ B$ .
    \includegraphics[width = 8cm]{s3.eps}

    Die Kurven $ \alpha,\beta,\delta$ seien definiert durch

    \begin{displaymath} \begin{array}{rlcl} \alpha: [0,2]\to\mathbb{R}^2\;, & \alpha... ... & \delta(t) & = & \displaystyle{t\choose t}\;. \\ \end{array}\end{displaymath}

    Dann wird $ B$ berandet durch die positive orientierte Kurve $ \gamma=\alpha-\beta-\delta$ . Mit dem Greenschen Integralsatz wird

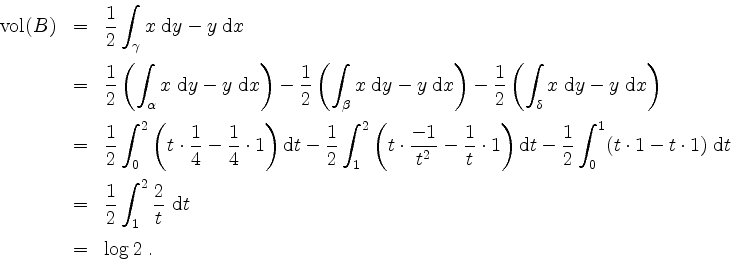
    \begin{displaymath} \begin{array}{rcl} \mathrm{vol}(B) & = & \dfrac{1}{2}\displa... ...ac{2}{t}\;\mathrm{d}t\vspace*{2mm}\\ &=& \log 2\;. \end{array}\end{displaymath}

    Die Koordinaten des Schwerpunkts $ (x_S,y_S)^\mathrm{t}$ von $ B$ ergeben sich mit Hilfe von 1. zu

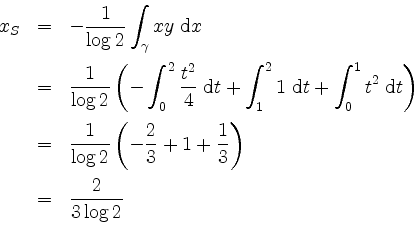
    \begin{displaymath} \begin{array}{rcl} x_S & = & -\dfrac{1}{\log 2}\displaystyl... ...{3}\right)\vspace*{2mm}\\ & = & \dfrac{2}{3\log 2} \end{array}\end{displaymath}

    und

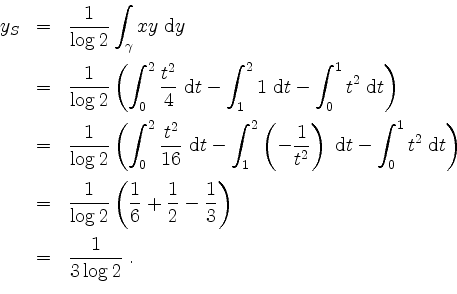
    \begin{displaymath} \begin{array}{rcl} y_S & = & \dfrac{1}{\log 2}\displaystyle\... ...3}\right)\vspace*{2mm}\\ &=& \dfrac{1}{3\log 2}\;. \end{array}\end{displaymath}

Als Probe prüfe man den resultierenden Schwerpunkt anhand der Skizze auf Plausibilität. Er sollte in $ B$ liegen, und dort auch nicht gerade am Rand.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006