Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1350: Zwei Oberflächenintegrale

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Gegeben sei das Vektorfeld $ v:\mathbb{R}^3\to\mathbb{R}^3$ , $ v(x,y,z)=(-y,x,x+y+z)^\mathrm{t}$ .

Bezeichne $ \Phi$ eine Fläche, deren Träger durch

$\displaystyle \{ (x,y,z)^\mathrm{t}\in\mathbb{R}^3\; \vert\; z + x^2 + y^2 = 1\; , z\ge 0\} $

gegeben ist.

Bezeichne $ \Psi$ eine Fläche, deren Träger durch

$\displaystyle \{ (x,y,z)^\mathrm{t}\in\mathbb{R}^3\; \vert\; x^2 + y^2 \le 1\; , z = 0\} $

gegeben ist.

Skizze des Trägers von $ \Phi$ .

\includegraphics[width = 8cm]{p4.eps}

Die Parametrisierung sei dabei so gewählt, daß der zugehörige Normalenvektor jeweils stets nicht nach unten zeige.

Berechne die Oberflächenintegrale $ \int_\Phi \mathrm{rot }v$ und $ \int_\Psi \mathrm{rot }v$ sowohl direkt als auch mit dem Stokesschen Integralsatz.

Wir verwende die Parametrisierungen

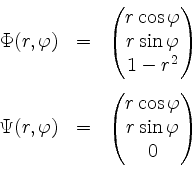
\begin{displaymath} \begin{array}{rcl} \Phi(r,\varphi) & = & \begin{pmatrix}r\co... ...pmatrix}r\cos\varphi\\ r\sin\varphi\\ 0\end{pmatrix}\end{array}\end{displaymath}

mit jeweils $ (r,\varphi)\in [0,1]\times [-\pi,\pi]$ .

Wir berechnen die Oberflächenintegrale zunächst mit dem Stokesschen Integralsatz.

Den Rand $ \partial K$ von $ K$ , der sich aus vier Geradenstücken zusammensetzt, beschreiben wir durch die folgenden vier ebenen Kurven.

\begin{displaymath} \begin{array}{rcll} \alpha(t) &=& (0,-t)^\mathrm{t}\; , & t\... ...t) &=& (-t,\pi)^\mathrm{t}\; , & t\in [-1,0]\;. \\ \end{array}\end{displaymath}

Der Rand $ \partial\Phi=\Phi\circ\partial K$ der Fläche $ \Phi$ wird also beschrieben durch die vier Raumkurven

\begin{displaymath} \begin{array}{rcll} (\Phi\circ\alpha)(t) &=& (0,\; 0,\; 1)^\... ...=& (t,\; 0,\;1-t^2)^\mathrm{t}\; , & t\in [-1,0]\;. \end{array}\end{displaymath}

Eine Betrachtung dieser Wege wird die Rechnung erleichtern. Zunächst ist $ \Phi\circ\alpha$ ein konstanter Weg, d.h. ein Kurvenintegral längs dieses Weges ist 0 . Ferner ist $ \Phi\circ\beta$ genau der zu $ \Phi\circ\delta$ entegegengestetzte Weg. Die Kurvenintegrale längs dieser beiden Wege heben sich gegenseitig auf. Es bleibt $ \Phi\circ\gamma$ zu betrachten. (Es bleibt also der anschaulich geometrische Rand von $ \Phi$ übrig.)

Der Rand $ \partial\Psi=\Psi\circ\partial K$ der Fläche $ \Psi$ wird also beschrieben durch die vier Raumkurven

\begin{displaymath} \begin{array}{rcll} (\Psi\circ\alpha)(t) &=& (0,\; 0,\; 0)^\... ...) &=& (t,\; 0,\; 0)^\mathrm{t}\; , & t\in [-1,0]\;. \end{array}\end{displaymath}

Zunächst ist $ \Psi\circ\alpha$ ein konstanter Weg, d.h. ein Kurvenintegral längs dieses Weges ist 0 . Ferner ist $ \Psi\circ\beta$ genau der zu $ \Psi\circ\delta$ entegegengestetzte Weg. Die Kurvenintegrale längs dieser beiden Wege heben sich gegenseitig auf. Bleibt $ \Psi\circ\gamma$ zu betrachten. (Es bleibt also der anschaulich geometrische Rand von $ \Psi$ übrig.)

Und es ist $ \Psi\circ\gamma = \Phi\circ\gamma$ . Wie also schon die Anschauung nahelegte, stimmen die rechten Seiten der Gleichung im Stokeschen Integralsatz für $ \Phi$ und für $ \Psi$ überein. Der Stokessche Integralsatz liefert somit

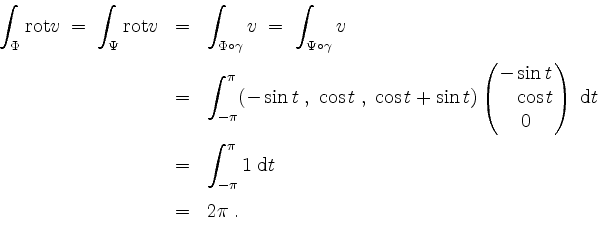
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_\Phi \mathrm{rot }v \;=... ...pi} 1\;\mathrm{d}t \vspace*{2mm}\\ & = & 2\pi \; . \end{array}\end{displaymath}

Für die direkte Rechnungen via $ \Phi$ und via $ \Psi$ bestimmen wir zunächst

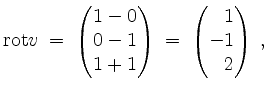
$\displaystyle \mathrm{rot }v \;=\; \begin{pmatrix}1-0\\ 0-1\\ 1+1\end{pmatrix}\;=\; \begin{pmatrix}\phantom{-}1\\ -1\\ \phantom{-}2\end{pmatrix}\;, $

sowie

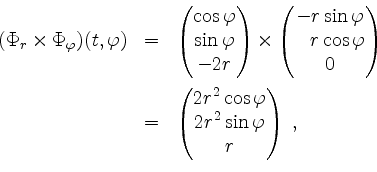
\begin{displaymath} \begin{array}{rcl} (\Phi_r \times \Phi_\varphi)(t,\varphi) &... ...2\cos\varphi\\ 2r^2\sin\varphi\\ r\end{pmatrix}\;, \end{array}\end{displaymath}

und entsprechend

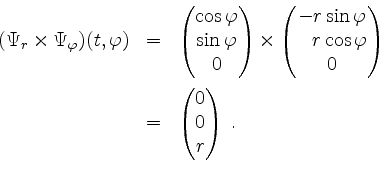
\begin{displaymath} \begin{array}{rcl} (\Psi_r \times \Psi_\varphi)(t,\varphi) &... ...\\ & = & \begin{pmatrix}0\\ 0\\ r\end{pmatrix} \;. \end{array}\end{displaymath}

Damit ist auch geklärt, daß der Normalenvektor jeweils nichtnegative dritte Koordinate hat, d.h. nicht nach unten zeigt.

Nach Definition des Oberflächenintegrals ist dann zum einen für $ \Phi$

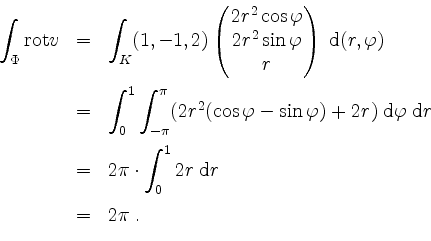
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_\Phi \mathrm{rot }v & =... ...2r\;\mathrm{d}r \vspace*{2mm}\\ & = & 2\pi \; .\\ \end{array}\end{displaymath}

Zum anderen wird für $ \Psi$

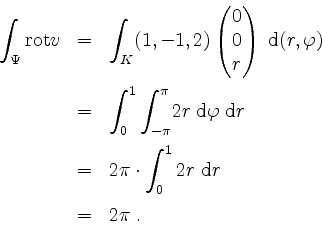
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_\Psi \mathrm{rot }v & =... ...2r\;\mathrm{d}r \vspace*{2mm}\\ & = & 2\pi \; .\\ \end{array}\end{displaymath}

Bemerkung: Da die Flächen $ \Phi$ und $ \Psi$ denselben anschaulich geometrischen Rand besitzen, folgt also nach dem Stokesschen Satz $ \int_\Phi \mathrm{rot }v = \int_\Psi \mathrm{rot }v$ . Dies liegt jedoch daran, daß sich die nicht-übereinstimmenden Teile nicht auf das Integral auswirken, was im allgemeinen nicht zu stimmen braucht.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006