
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1351: Ein Kurvenintegral |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Sei
![]() definiert durch
definiert durch
![]() .
.
Sei das Vektorfeld
![]() definiert durch
definiert durch
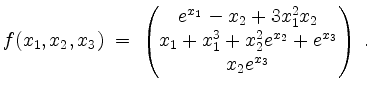
Berechne das Kurvenintegral
Sei
![]() definiert durch
definiert durch
![]() .
.
Skizze des Trägers von ![]() .
.
![\includegraphics[width = 8cm]{s5.eps}](/inhalt/loesung/loesung724/img4.png)
Den Rand
![]() von
von ![]() , der sich aus vier Geradenstücken zusammensetzt,
beschreiben wir durch die folgenden vier ebenen Kurven.
, der sich aus vier Geradenstücken zusammensetzt,
beschreiben wir durch die folgenden vier ebenen Kurven.
![\begin{displaymath}
\begin{array}{rcll}
\alpha(t) &=& (0,-t)^\mathrm{t}\; , & t\...
...t) &=& (-t,\pi)^\mathrm{t}\; , & t\in [-1,0]\;. \\
\end{array}\end{displaymath}](/inhalt/loesung/loesung724/img7.png)
Der Rand
![\begin{displaymath}
\begin{array}{rcll}
(\Phi\circ\alpha)(t) &=& (0,\; 0,\; 0)^\...
...) &=& (t,\; 0,\;-t)^\mathrm{t}\; , & t\in [-1,0]\;.
\end{array}\end{displaymath}](/inhalt/loesung/loesung724/img9.png)
Eine Betrachtung dieser Wege wird die Rechnung erleichtern. Zunächst ist
Weiterhin berechnen wir die Rotation von ![]() zu
zu
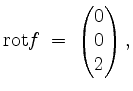
sowie den Normalenvektor
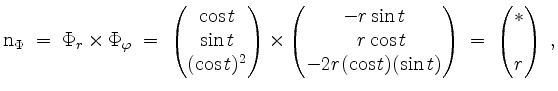
desssen oberen beiden Einträge uns nicht interessieren.
Der Stokessche Integralsatz liefert unter Beachtung der Tatsache, daß nur
![]() einen relevanten
Beitrag zum Kurvenintegral längs
einen relevanten
Beitrag zum Kurvenintegral längs
![]() liefert, also
liefert, also
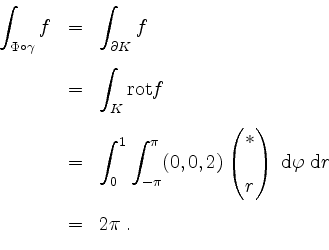
| automatisch erstellt am 11. 8. 2006 |