
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1352: Gaußscher Integralsatz |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Es sei
![]() . Berechne
für das Vektorfeld
. Berechne
für das Vektorfeld
![]() definiert durch
definiert durch
![]() das Integral
das Integral
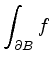
Dabei sei der Rand
![]() so parametrisiert, daß der Normalenvektor stets nach außen zeige.
so parametrisiert, daß der Normalenvektor stets nach außen zeige.
![$\displaystyle \Phi^{(1)}: \underbrace{[0,2] \times [0,2\pi]}_{=:\; K^{(1)}} \to...
...,\varphi) := \begin{pmatrix}r \sin \varphi\\ r \cos \varphi\\ 0 \end{pmatrix},
$](/inhalt/loesung/loesung726/img4.png)
sowie
![$\displaystyle \Phi^{(2)}: \underbrace{[0,2] \times [0,2\pi]}_{=:\; K^{(2)}} \to...
...rphi) := \begin{pmatrix}r \cos \varphi\\ r \sin \varphi\\ 4-r^2 \end{pmatrix}.
$](/inhalt/loesung/loesung726/img5.png)
Die unterschiedliche Wahl der ersten Komponenten mag zunächst ungewöhnlich erscheinen, ist jedoch dadurch bedingt, daß wir garantieren möchten, daß die folgenden Normalenvektoren der Flächen
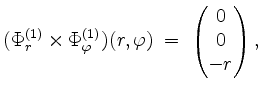
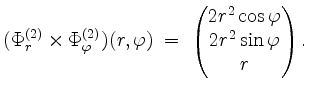
Nun ist
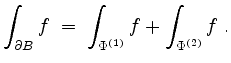
Folglich berechnen wir
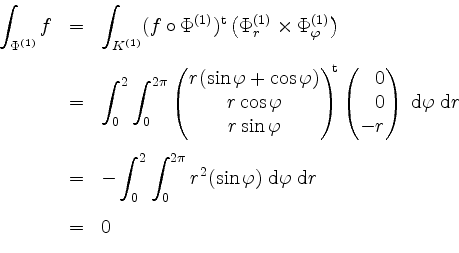
und
![\begin{displaymath}
\begin{array}{rcl}
\displaystyle \int_{\Phi^{(2)}} f
&=& \di...
... + 2r^2 \right]_0^2 \vspace{3mm}\\
&=& 24 \pi \; .
\end{array}\end{displaymath}](/inhalt/loesung/loesung726/img12.png)
Wir haben also berechnet, daß
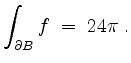
![\begin{displaymath}
\begin{array}{rcl}
\displaystyle \int_{\partial B} f
&=& \d...
...{r^4}{4} \right]_0^2\vspace{3mm}\\
&=& 24 \pi \; .
\end{array}\end{displaymath}](/inhalt/loesung/loesung726/img15.png)
| automatisch erstellt am 11. 8. 2006 |