Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1355: Differentiation und Integration von Fourierreihen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

1.
Berechne die Fourierreihe der $ 2\pi$ -periodischen Funktion $ f:\mathbb{R}\to\mathbb{R}$ , welche gegeben ist durch

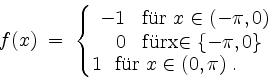
\begin{displaymath} f(x)\;=\; \left\{ \begin{array}{rl} -1 & \mbox{f''ur $x\... ... \\ 1 & \mbox{f''ur $x\in (0,\pi)\;$}. \end{array}\right. \end{displaymath}

An welchen Stellen haben die Funktion und ihre Fourierreihe denselben Wert?
2.
Berechne die Fourierreihe der $ 2\pi$ -periodischen Funktion $ g:\mathbb{R}\to\mathbb{R}$ , welche gegeben ist durch

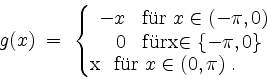
\begin{displaymath} g(x)\;=\; \left\{ \begin{array}{rl} -x & \mbox{f''ur $x\... ... \\ x & \mbox{f''ur $x\in (0,\pi)\; $}. \end{array}\right. \end{displaymath}

Verwende hierzu die Fourierreihe aus 1.

1.
Die Funktion ist ungerade, daher ist stets $ a_k = 0\,$ .

Die Funktionswerte von $ f$ in $ \{0,\pi\}$ spielen für die Berechnung der Koeffizienten $ b_k$ keine Rolle. Wir erhalten für $ k\geq 1$

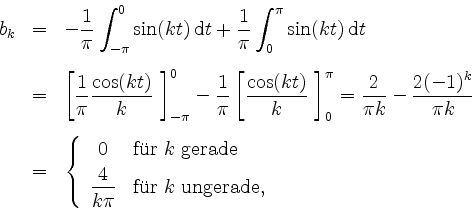
\begin{displaymath} \begin{array}{rcl} b_k & = & -\dfrac{1}{\pi}\displaystyl... ...box{f''ur $k$\ ungerade,}\\ \end{array}\right. \end{array} \end{displaymath}

woraus sich die Fourierreihe

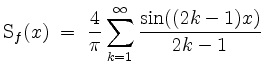
$\displaystyle \mathrm{S}_f(x) \;=\; \frac{4}{\pi}\sum_{k=1}^\infty\frac{\sin((2k-1)x)}{2k-1} $

ergibt.

In $ (-\pi,0)\cup (0,\pi)$ ist $ f$ differenzierbar, dort ist also $ \mathrm{S}_f(x) = f(x)$ .

Ist $ x\in\pi\mathbb{Z}$ , so hat $ f$ in $ x$ einen links- und rechtsseitigen Grenzwert, und ist links- und rechtsseitig differenzierbar. Als Wert der Fourierreihe ergibt sich das arithmetische Mittel des linksseitigen und des rechtsseitigen Grenzwerts, nämlich 0 . Dies ist zugleich der Funktionswert von $ f$ in $ x$ . Also ist auch hier $ \mathrm{S}_f(x) = f(x)$ .

Insgesamt ist $ \mathrm{S}_f(x) = f(x)$ für alle $ x\in\mathbb{R}$ .

Skizze des Graphen der ersten $ 3$ und des Graphen der ersten $ 20$ Summanden der Fourierreihe.

Skizze des Graphen der ersten $ 1000$ Summanden der Fourierreihe in der Nähe von $ x = 0$ .

2.
Die Funktion $ g$ ist auf $ (-\pi,\pi)$ bis auf die Ausnahmestelle 0 stetig differenzierbar, also gilt dort $ g'=f\,$ . An der Ausnahmestelle 0 ist $ g$ stetig und besitzt eine links- und rechtsseitige Ableitung, nämlich $ -1$ und $ 1$ , deren Mittelwert gerade $ 0=f(0)$ ist. Also erhalten wir durch summandenweises Aufleiten

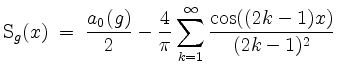
$\displaystyle \mathrm{S}_g(x) \;=\; \frac{a_0(g)}{2} - \frac{4}{\pi}\sum_{k=1}^\infty\frac{\cos((2k-1)x)}{(2k-1)^2} $

mit

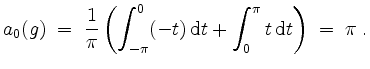
$\displaystyle a_0(g) \;=\; \frac{1}{\pi}\left(\int_{-\pi}^0 (-t)\,\mathrm{d}t + \int_0^{\pi} t\,\mathrm{d}t\right) \;=\; \pi \; . $

Insgesamt wird also

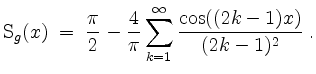
$\displaystyle \mathrm{S}_g(x) \;=\; \frac{\pi}{2} - \frac{4}{\pi}\sum_{k=1}^\infty\frac{\cos((2k-1)x)}{(2k-1)^2}\; . $

Skizze des Graphen der ersten $ 2$ und des Graphen der ersten $ 10$ Summanden der Fourierreihe.

Skizze des Graphen der ersten $ 40$ und des Graphen der ersten $ 800$ Summanden der Fourierreihe in der Nähe von $ x = 0$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006