Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1357: Fourierentwicklung zur Berechnung von Werten verschiedener Reihen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

1.
Berechne die komplexe Fourierentwicklung von $ f(x) = x^2$ auf $ [0,2\pi)$ , $ 2\pi$ -periodisch fortgesetzt.
2.
Berechne die komplexe Fourierentwicklung von $ g(x) = x^3$ auf $ [0,2\pi)$ , $ 2\pi$ -periodisch fortgesetzt.
3.
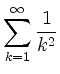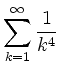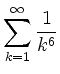Bestimme $ \displaystyle\sum_{k = 1}^\infty \frac{1}{k^2}$ , $ \displaystyle\sum_{k = 1}^\infty \frac{1}{k^4}$ und $ \displaystyle\sum_{k = 1}^\infty \frac{1}{k^6}$ aus Parsevalschen Norm- und Skalarproduktgleichungen dieser beiden Funktionen.

1.
Wir erhalten für $ k\ne 0$

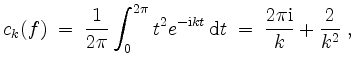
$\displaystyle c_k(f) \;=\; \frac{1}{2\pi} \int_0^{2\pi} t^2 e^{-\mathrm{i} kt}\,\mathrm{d}t \;=\; \frac{2\pi\mathrm{i}}{k} + \frac{2}{k^2}\; , $

sowie

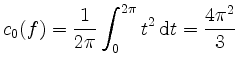
$\displaystyle c_0(f) = \frac{1}{2\pi} \int_0^{2\pi} t^2 \,\mathrm{d}t = \frac{4\pi^2}{3} $

und somit

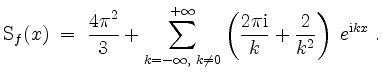
$\displaystyle \mathrm{S}_f(x) \;=\; \frac{4\pi^2}{3} + \sum_{k = -\infty,\; k\n... ...\left(\frac{2\pi\mathrm{i}}{k} + \frac{2}{k^2}\right)\; e^{\mathrm{i} kx} \; . $

Skizze des Graphen der ersten $ 4$ und des Graphen der ersten $ 40$ Summanden der zugehörigen reellen Fourierreihe

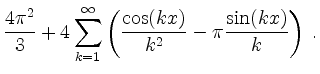
$\displaystyle \frac{4\pi^2}{3} + 4\sum_{k = 1}^\infty \left(\frac{\cos(kx)}{k^2} - \pi \frac{\sin(kx)}{k}\right)\; . $

\includegraphics[width = 12cm]{quad_per.eps}

2.
Wir erhalten für $ k\ne 0$

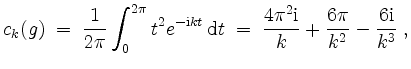
$\displaystyle c_k(g) \;=\; \frac{1}{2\pi} \int_0^{2\pi} t^2 e^{-\mathrm{i} kt}\... ...\; \frac{4\pi^2\mathrm{i}}{k} + \frac{6\pi}{k^2} - \frac{6\mathrm{i}}{k^3}\; , $

sowie

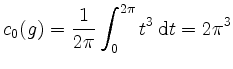
$\displaystyle c_0(g) = \frac{1}{2\pi} \int_0^{2\pi} t^3 \,\mathrm{d}t = 2\pi^3 $

und somit

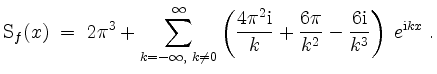
$\displaystyle \mathrm{S}_f(x) \;=\; 2\pi^3 + \sum_{k = -\infty,\; k\ne 0}^{\inf... ...} + \frac{6\pi}{k^2} - \frac{6\mathrm{i}}{k^3}\right)\; e^{\mathrm{i} kx} \; . $

Skizze des Graphen der ersten $ 4$ und des Graphen der ersten $ 40$ Summanden der zugehörigen reellen Fourierreihe

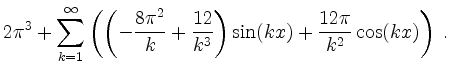
$\displaystyle 2\pi^3 + \sum_{k = 1}^\infty \left(\left(-\frac{8\pi^2}{k} + \frac{12}{k^3}\right)\sin(kx) + \frac{12\pi}{k^2}\cos(kx)\right) \; . $

\includegraphics[width = 12cm]{cube_per.eps}

3.
Die Parsevalsche Skalarproduktgleichung ergibt für $ f$ und $ g$

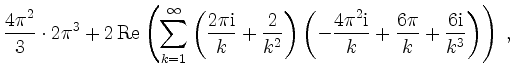
$\displaystyle \frac{4\pi^2}{3}\cdot 2\pi^3 + 2\,\mathrm{Re}\left(\sum_{k = 1}^\... ...^2\mathrm{i}}{k} + \frac{6\pi}{k} + \frac{6\mathrm{i}}{k^3}\right)\right) \; , $

also

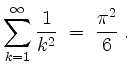
$\displaystyle \sum_{k = 1}^\infty \frac{1}{k^2} \;=\; \frac{\pi^2}{6}\; . $

Die Parsevalsche Normgleichung ergibt für $ f$

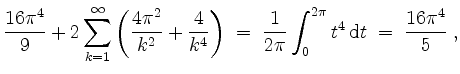
$\displaystyle \frac{16\pi^4}{9} + 2\sum_{k = 1}^\infty\left(\frac{4\pi^2}{k^2} ... ...\;=\; \frac{1}{2\pi}\int_0^{2\pi} t^4\,\mathrm{d}t \;=\; \frac{16\pi^4}{5}\; , $

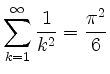also, unter Verwendung von $ \displaystyle\sum_{k = 1}^\infty \frac{1}{k^2} = \frac{\pi^2}{6}$ ,

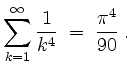
$\displaystyle \sum_{k = 1}^\infty \frac{1}{k^4} \;=\; \frac{\pi^4}{90}\; . $

Die Parsevalschen Normgleichung ergibt für $ g$

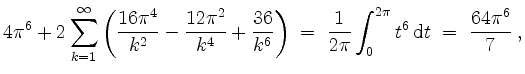
$\displaystyle 4\pi^6 + 2\sum_{k = 1}^\infty\left(\frac{16\pi^4}{k^2} - \frac{12... ...;=\; \frac{1}{2\pi}\int_0^{2\pi} t^6\,\mathrm{d}t \;=\; \frac{64\pi^6}{7}\; , $

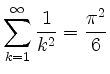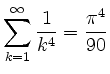also, unter Verwendung von $ \displaystyle\sum_{k = 1}^\infty \frac{1}{k^2} = \frac{\pi^2}{6}$ und von $ \displaystyle\sum_{k = 1}^\infty \frac{1}{k^4} = \frac{\pi^4}{90}$ ,

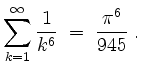
$\displaystyle \sum_{k = 1}^\infty \frac{1}{k^6} \;=\; \frac{\pi^6}{945}\; . $

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006