Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1358: Fouriertransformation, Parsevalsche Gleichung, Poissonsche Summenformel

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei $ f(t) := (t^2 + 1)^{-1}$ .

(1)
Berechne die Fouriertransformierte von $ f(t)$ .
(2)
Berechne die Fouriertransformierte von $ t f(t)^2$ .
(3)
Berechne die Fouriertransformierte von $ t^2 f(t)^2$ .
(4)
Bestätige im vorliegenden Fall durch direkte Rechnung, daß $ (f^\wedge)^\wedge(t) = 2\pi\cdot f(-t)$ .
(5)
Verwende die Parsevalsche Gleichung zur Berechnung von $ \int_{-\infty}^{+\infty} (t^2 + 1)^{-2}\,\mathrm{d}t$ .
(6)
Verwende die Poissonsche Summationsformel zur Berechnung von $ \sum_{n = 1}^\infty (1 + n^2)^{-1}$ .

(1)
Wir wollen

$\displaystyle \hat{f}(\omega) \; =\; [(t^2 + 1)^{-1}]^\wedge(\omega) \; =\; {\d... ...\int_{-\infty}^{+\infty}}\frac{e^{-\mathrm{i}\omega t}}{t^2 + 1} \,\mathrm{d}t $

berechnen, zunächst für $ \omega > 0$ .

Sei $ R > 0$ . Sei $ \gamma_{1,R}(s) := Rs - R(1-s) = R(2s-1)$ für $ s\in [0,1]$ . Sei $ \gamma_{2,R}(s) := R\exp(-\pi\mathrm{i} s)$ für $ s\in [0,1]$ . Sei $ \gamma_R = \gamma_{1,R} + \gamma_{2,R}$ . Es durchläuft also $ \gamma_R$ den Rand eines Halbkreises von Radius $ R$ mit dem Ursprung als Mittelpunkt, welcher in der unteren Halbebene liegt.

Zunächst halten wir fest, daß

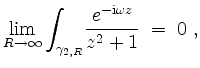
$\displaystyle \lim_{R\to\infty} {\displaystyle\int_{\gamma_{2,R}}}\frac{e^{-\mathrm{i}\omega z}}{z^2 + 1} \; =\; 0\;, $

da für $ R\ge\sqrt{2}$ sich

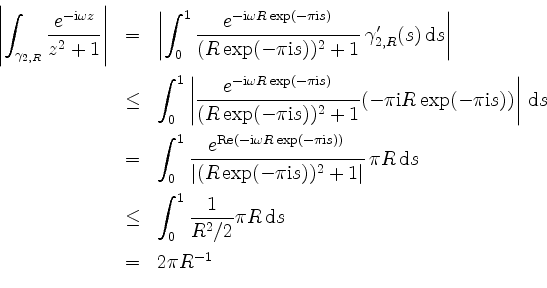
\begin{displaymath} \begin{array}{rcl} \left\vert\displaystyle\int_{\gamma_{2,R}... ...\mathrm{d}s \vspace*{2mm} \\ & = & 2\pi R^{-1} \\ \end{array}\end{displaymath}

ergibt. Ferner ist

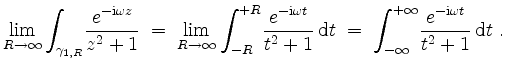
$\displaystyle \lim_{R\to\infty} {\displaystyle\int_{\gamma_{1,R}}}\frac{e^{-\ma... ...t_{-\infty}^{+\infty}}\frac{e^{-\mathrm{i}\omega t}}{t^2 + 1}\,\mathrm{d}t\; . $

Insgesamt ist also, da $ \int_{\gamma_R} = \int_{\gamma_{1,R}} + \int_{\gamma_{2,R}}$ ,

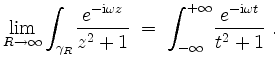
$\displaystyle \lim_{R\to\infty} {\displaystyle\int_{\gamma_R}}\frac{e^{-\mathrm... ...splaystyle\int_{-\infty}^{+\infty}}\frac{e^{-\mathrm{i}\omega t}}{t^2 + 1}\; . $

Der Integrand hat in der unteren Halbebene nur eine Singularität bei $ -\mathrm{i}$ , namentlich einen Pol erster Ordnung, und dort ist

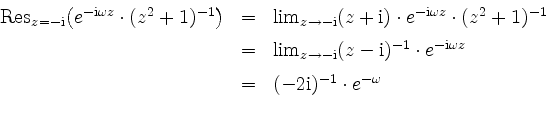
\begin{displaymath} \begin{array}{rcl} \mathrm{Res}_{z = -\mathrm{i}}\big(e^{-\m... ...2\mathrm{i})^{-1}\cdot e^{-\omega} \vspace*{2mm}\\ \end{array}\end{displaymath}

Mit dem Residuensatz wird nun wegen der negativen Umlaufrichtung von $ \gamma_R$ für $ R > 1$ um die Singularität bei $ -\mathrm{i}$

\begin{displaymath} \begin{array}{rcl} [(t^2 + 1)^{-1}]^\wedge(\omega) & = & {\d... ...\vspace*{2mm}\\ & = & \pi\cdot e^{-\omega}\; . \\ \end{array}\end{displaymath}

Da nun $ \hat{f}(\omega) = [f(t)]^\wedge(\omega) = [f(-t)]^\wedge(\omega) = \hat{f}(-\omega)$ , folgt für $ \omega\in\mathbb{R}$ , daß

$\displaystyle \hat{f}(\omega) \; =\; [(t^2 + 1)^{-1}]^\wedge(\omega) \; =\; \pi\cdot e^{-\vert\omega\vert} $

(2)
Zunächst einmal merken wir an, daß $ f'(t) = -2t (1+t^2)^{-2} = -2t f(t)^2$ , und daß

$\displaystyle [f'(t)]^\wedge(\omega) \; =\; \mathrm{i}\omega\hat{f}(\omega) \; =\; \mathrm{i}\omega\pi\cdot e^{-\vert\omega\vert}\; , $

so daß sich

$\displaystyle [tf(t)^2]^\wedge(\omega) \; =\; -\frac{\pi\mathrm{i}}{2}\cdot\omega\cdot e^{-\vert\omega\vert} $

ergibt.

(3)
Mit (2) ergibt sich

\begin{displaymath} \begin{array}{rcl} [t^2 f(t)^2]^\wedge(\omega) & = & [t \cdo... ...\vert)\, e^{-\vert\omega\vert}\; . \vspace*{2mm}\\ \end{array}\end{displaymath}

(4)
Mit (1) bleibt zu zeigen, daß

$\displaystyle [e^{-\vert\omega\vert}]^\wedge (t) \;\overset{!}{=}\; 2f(-t) \; =\; 2 (1 + t^2)^{-1}\; . $

In der Tat wird

\begin{displaymath} \begin{array}{rcl} [e^{-\vert\omega\vert}]^\wedge (t) & = & ... ...-1} \vspace*{4mm}\\ & = & 2 (1 + t^2)^{-1}\; . \\ \end{array}\end{displaymath}

(5)
Die Parsevalsche Gleichung besagt hier, daß

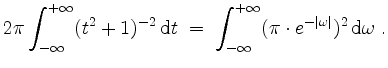
$\displaystyle 2\pi\int_{-\infty}^{+\infty} (t^2 + 1)^{-2}\,\mathrm{d}t \; =\; \int_{-\infty}^{+\infty} (\pi\cdot e^{-\vert\omega\vert})^2\,\mathrm{d}\omega\; . $

Daraus kann man folgern, daß

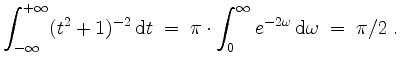
$\displaystyle \int_{-\infty}^{+\infty} (t^2 + 1)^{-2}\,\mathrm{d}t \; =\; \pi\cdot\int_0^\infty e^{-2\omega}\,\mathrm{d}\omega\; =\; \pi/2 \; . $

Dies hätte man auch mittels Partialbruchzerlegung oder mittels Residuensatz erhalten können.

(6)
Die Poissonsche Summationsformel gibt hier

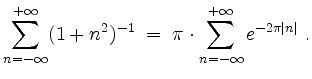
$\displaystyle \sum_{n = -\infty}^{+\infty} (1 + n^2)^{-1} \; =\; \pi\cdot \sum_{n = -\infty}^{+\infty} e^{-2\pi \vert n\vert}\; . $

Demzufolge wird

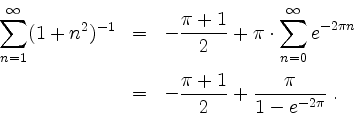
\begin{displaymath} \begin{array}{rcl} {\displaystyle\sum_{n = 1}^\infty} (1 + n... ...c{\pi + 1}{2} + \dfrac{\pi}{1 - e^{-2\pi}} \; . \\ \end{array}\end{displaymath}

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006