Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1359: Fouriertransformation

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei eine absolut integrierbare Funktion $ f:\mathbb{R}\to\mathbb{C}$ gegeben.

Es sei eine Funktion $ x:\mathbb{R}\to\mathbb{C}$ gesucht mit

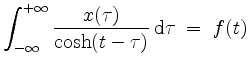
$\displaystyle \int_{-\infty}^{+\infty} \frac{x(\tau)}{\cosh(t - \tau)}\,\mathrm{d}\tau \; =\; f(t) $

für $ t\in\mathbb{R}$ .

Leite die Lösung

$\displaystyle x(t) \; =\; \dfrac{1}{2\pi^2}\, [\hat{f}(\omega)\cosh(\omega\pi/2)]^\wedge(-t)\; . $

her.

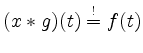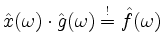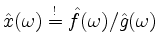Schreibe $ g(t) := 1/\cosh(t)$ . Zu lösen ist $ (x\ast g)(t) \overset{!}{=} f(t)$ . Mittels Fouriertransformation gibt dies $ \hat{x}(\omega)\cdot \hat{g}(\omega) \overset{!}{=} \hat{f}(\omega)$ , also $ \hat{x}(\omega) \overset{!}{=} \hat{f}(\omega)/\hat{g}(\omega)$ . Fouriertransformieren wir dies abermals, so wird $ 2\pi\cdot x(-t) \;\overset{!}{=}\; [\hat{f}(\omega)/\hat{g}(\omega)]^\wedge(t)$ , d.h.

$\displaystyle x(t) \; =\; \dfrac{1}{2\pi}\, [\hat{f}(\omega)/\hat{g}(\omega)]^\wedge(-t)\; . $

Wir müssen nun noch $ \hat{g}(\omega)$ berechnen. Sei zunächst $ \omega > 0$ . Es wird

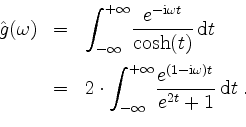
\begin{displaymath} \begin{array}{rcl} \hat{g}(\omega) & = & {\displaystyle\int_... ...hrm{i}\omega) t}}{e^{2t} + 1}\,\mathrm{d}t \; . \\ \end{array}\end{displaymath}

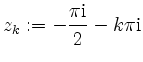Der Integrand hat einfache Polstellen bei $ z_k := -\dfrac{\pi\mathrm{i}}{2} - k\pi\mathrm{i}$ für $ k\in\mathbb{Z}$ , mit Residuum

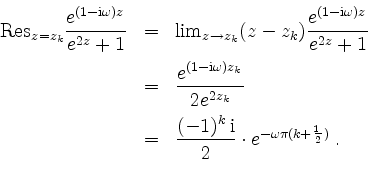
\begin{displaymath} \begin{array}{rcl} \mathrm{Res}_{z = z_k} \dfrac{e^{(1-\math... ...i}}{2}\cdot e^{-\omega\pi(k + \frac{1}{2})}\; . \\ \end{array}\end{displaymath}

Integrieren wir für $ R > 0$ in negativer Umlaufrichtung über das Rechteck $ (+R,\, -R,\, -R-\mathrm{i} R,\, R-\mathrm{i} R)$ , bezeichnen diesen Weg mit $ \gamma_R$ , und lassen $ R\to\infty$ laufen, wobei $ R$ nur ganzzahlige Vielfache von $ \pi$ als Werte annehme, so wird mit dem Residuensatz und geometrischer Reihe

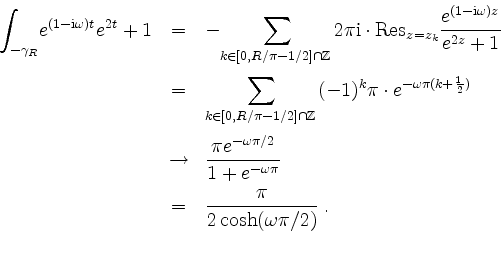
\begin{displaymath} \begin{array}{rcl} {\displaystyle\int_{-\gamma_R}} \fracd{e^... ...frac{\pi}{2\cosh(\omega\pi/2)}\; . \vspace*{2mm}\\ \end{array}\end{displaymath}

Eine Grenzwertbetrachtung ergibt, daß die Integralanteile auf den nicht auf der reellen Achse liegenden Seiten unseres Rechtecks mit $ R\to\infty$ gegen 0 streben. In der Tat ist in

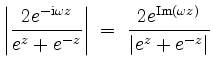
$\displaystyle \left\vert\dfrac{2e^{-\mathrm{i}\omega z}}{e^z + e^{-z}}\right\vert \; =\; \dfrac{2e^{\mathrm{Im}(\omega z)}}{\vert e^z + e^{-z}\vert} $

der Nenner groß und der Zähler nach oben beschränkt auf den beiden vertikalen Seiten des Rechtecks, und der Zähler klein und der Nenner nach unten beschränkt auf der unteren horizontalen Seite des Rechtecks - beachte für letzteres, daß $ R$ ein ganzzahliges Vielfaches von $ \pi$ ist.

Also ist

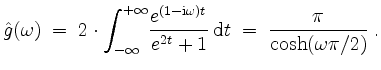
$\displaystyle \hat{g}(\omega) \; =\; 2\cdot {\displaystyle\int_{-\infty}^{+\inf... ...mega) t}}{e^{2t} + 1}\,\mathrm{d}t \; = \; \dfrac{\pi}{\cosh(\omega\pi/2)}\; . $

Wegen Symmetrie und Stetigkeit gilt dies für alle $ \omega\in\mathbb{R}$ .

Insgesamt erhalten wir in der Tat

$\displaystyle x(t) \; =\; \dfrac{1}{2\pi^2}\, [\hat{f}(\omega)\cosh(\omega\pi/2)]^\wedge(-t)\; . $

Es handelt sich um ein Beispiel einer fredholmschen Integralgleichung.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006