Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1363: Ein inhomogenes System linearer Differentialgleichungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

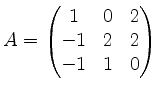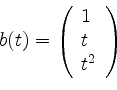Es seien $ A=\begin{pmatrix}1&0&2\\ -1&2&2\\ -1&1&0\end{pmatrix}$ und \begin{displaymath}b(t) = \left( \begin{array}{l} 1 \\ t \\ t^2 \\ \end{array}\right)\end{displaymath} .

Löse die Differentialgleichung $ x'(t) = Ax(t) + b(t)\,$ .

Wir berechnen zunächst

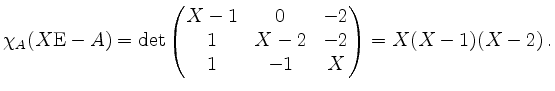
$\displaystyle \chi_A(X\mathrm{E}-A)=\det\begin{pmatrix}X-1&0&-2\\ 1&X-2&-2\\ 1&-1&X\end{pmatrix}=X(X-1)(X-2)\,.$

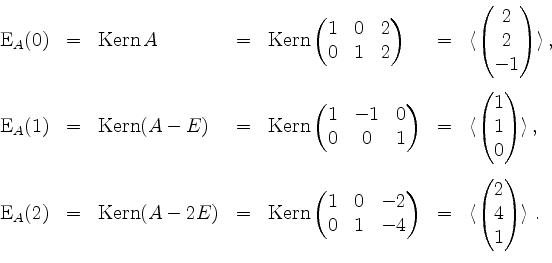
Also hat $ A$ die Eigenwerte $ 0,1,2\,$ und ist somit diagonalisierbar. Nun ist

\begin{displaymath} \begin{array}{rclclcl} \mathrm{E}_A(0) & = &\operatorname{Ke... ...begin{pmatrix}2\\ 4\\ 1\end{pmatrix}\rangle \; .\\ \end{array}\end{displaymath}

Mit

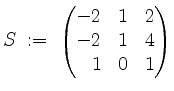
$\displaystyle S \; :=\; \begin{pmatrix}-2&1&2\\ -2&1&4\\ \hfill 1&0&1\end{pmatrix}$

wird also

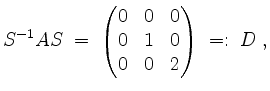
$\displaystyle S^{-1}AS\; =\; \begin{pmatrix}0&0&0\\ 0&1&0\\ 0&0&2\end{pmatrix} \; =:\; D\; , $

und somit

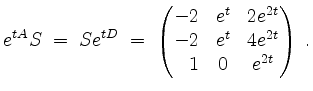
$\displaystyle e^{tA}S\; =\; S e^{tD} \; = \; \begin{pmatrix}-2&e^t&2e^{2t}\\ -2&e^t&4e^{2t}\\ \hfill 1&0&e^{2t}\end{pmatrix}\; . $

Die allgemeine Lösung der zugehörigen homogenen Gleichung $ x'(t) = A x(t)$ lautet somit

$\displaystyle x(t)\; =\; e^{tA}Sc $

mit einem Vektor $ c\in\mathbb{C}^3\,$ .

Variation der Konstanten sieht den Ansatz

$\displaystyle x(t)\; =\; e^{tA}Sc(t) \;=\; S e^{tD} c(t) $

vor. Einsetzen in die ursprüngliche Gleichung $ x'(t) = Ax(t) + b(t)$ liefert die Bedingung

$\displaystyle A e^{tA} Sc + e^{tA} S c' \; =\; A e^{tA} Sc + b\; , $

i.e. die Bedingung

$\displaystyle e^{tA} S c' \; =\; b $

an $ c(t)$ . Wir berechnen die Partikulärlösung

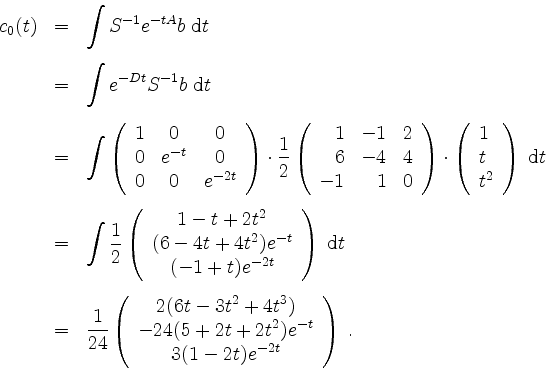
\begin{displaymath} \begin{array}{rcl} c_0(t) & = & \displaystyle\int S^{-1} e^... ...\ 3(1 - 2t)e^{-2t} \\ \end{array}\right) \; . \\ \end{array}\end{displaymath}

Hieraus erhalten wir die Partikulärlösung

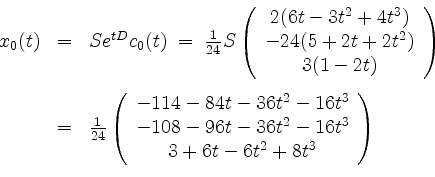
\begin{displaymath} \begin{array}{rcl} x_0(t) &=& S e^{tD} c_0(t) \; =\; \frac{1... ...\\ 3 + 6 t - 6 t^2 + 8 t^3 \\ \end{array}\right) \end{array}\end{displaymath}

der ursprünglichen inhomogenen Gleichung $ x'(t) = Ax(t) + b(t)$ .

Die allgemeine Lösung ergibt sich nun als Summe der partikulären inhomogenen Lösung $ x_0(t)$ und der allgemeinen homogenen Lösung $ e^{tA}Sc$ zu

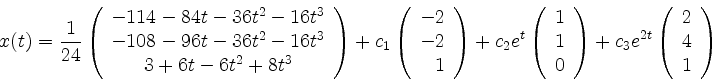
\begin{displaymath} x(t)=\frac{1}{24} \left( \begin{array}{c} -114 - 84 t - 36 ... ...eft( \begin{array}{r} 2 \\ 4 \\ 1 \\ \end{array}\right) \end{displaymath}

für beliebig gewählte Konstanten $ c_1,\, c_2,\, c_3\,\in\,\mathbb{C}$ .
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 22.  8. 2006