Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1366: Eine inhomogene lineare Differentialgleichung zweiter Ordnung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Löse die Differentialgleichung $ y''(t)-y(t)=e^{2t}(1+t)\,$ .

Wir lösen zunächst die zugehörige homogene Differentialgleichung, deren charakteristisches Polynom sich zu

$\displaystyle \chi(X) \;=\; X^2-1 \;=\; (X+1)(X-1) $

faktorisiert. Also ist

$\displaystyle (\; e^{-t}, \; e^t \; ) $

eine Basis des Lösungsraumes, und $ y_h(t)=c_1e^{-t}+c_2e^t$ mit $ c_1,c_2\in\mathbb{C}$ die allgemeine Lösung der zugehörigen homogenen Differentialgleichung $ y''(t) - y(t) = 0$ .

Da die Störfunktion in der Differentialgleichung eine einfache Gestalt hat, machen wir einen Ansatz vom Typ der rechten Seite für die partikuläre Lösung. Sei also

$\displaystyle y_\mathrm{p}(t) \;=\; e^{2t}(A_1t+A_0) $

mit noch zu bestimmenden Koeffizienten $ A_0,\, A_1\,\in\,\mathbb{C}$ .

Damit wird

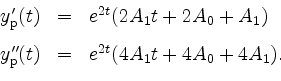
\begin{displaymath} \begin{array}{rcl} y_\mathrm{p}'(t) &=& e^{2t}(2A_1t+2A_0+A_... ...}\\ y_\mathrm{p}''(t) &=& e^{2t}(4A_1t+4A_0+4A_1). \end{array}\end{displaymath}

Durch Einsetzen von $ y_\mathrm{p}(t)$ in die Differentialgleichung erhalten wir die Bedingung

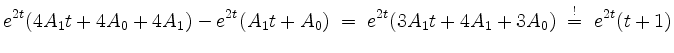
$\displaystyle e^{2t}(4A_1t + 4A_0 + 4A_1)-e^{2t}(A_1t + A_0) \;=\; e^{2t}(3A_1t + 4A_1 + 3A_0)\;\overset{!}{=}\; e^{2t}(t + 1) $

und folgern durch Koeffizientenvergleich

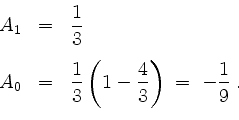
\begin{displaymath} \begin{array}{rcl} A_1 &=& \dfrac{1}{3}\vspace{3mm}\\ A_0 &... ...\left(1-\dfrac{4}{3}\right)\; =\; -\dfrac{1}{9}\; . \end{array}\end{displaymath}

Also ist

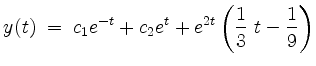
$\displaystyle y(t) \;=\; c_1e^{-t}+c_2e^t+e^{2t}\left(\frac{1}{3}\;t-\frac{1}{9}\right) $

für $ c_1,\, c_2\,\in\,\mathbb{C}$ die allgemeine Lösung der gegebenen Differentialgleichung.
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006