
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1367: Eine inhomogene lineare Differentialgleichung zweiter Ordnung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Bestimme alle Lösungen der Differentialgleichung
![]() .
.
Das charakteristische Polynom der zugehörigen homogenen Differentialgleichung ist
Also ist
des Lösungsraumes.
Die rechte Seite der Differentialgleichung hat keine einfache Gestalt, also verwenden wir die Methode der Variation der Konstanten. Für eine partikuläre Lösung setzen wir demgemäß
mit noch zu bestimmenden Funktionen
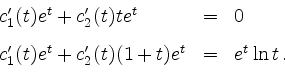
Eine Betrachtung der Differenz gibt
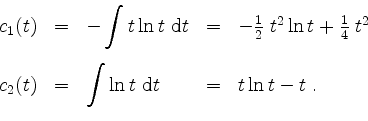
Die allgemeine Lösung setzt sich nun zusammen zu
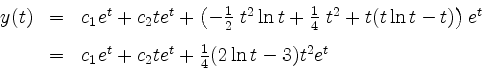
mit
| automatisch erstellt am 11. 8. 2006 |