Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1369: Ein inhomogenes System von sieben linearen Differentialgleichungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Es seien

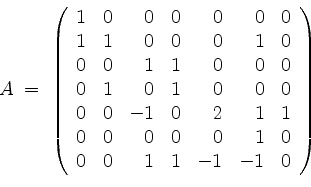
\begin{displaymath} A \; =\; \left( \begin{array}{rrrrrrr} 1 & 0 & 0 & 0 & 0 & ... ...& 1 & 0 \\ 0 & 0 & 1 & 1 &-1 &-1 & 0 \\ \end{array}\right) \end{displaymath}

und

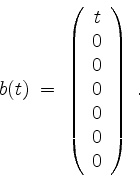
\begin{displaymath} b(t) \; =\; \left( \begin{array}{c} t \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array}\right) \; . \end{displaymath}

Löse die Differentialgleichung $ u'(t) = Au(t) + b(t)$ .

Das charakteristische Polynom ergibt sich zu

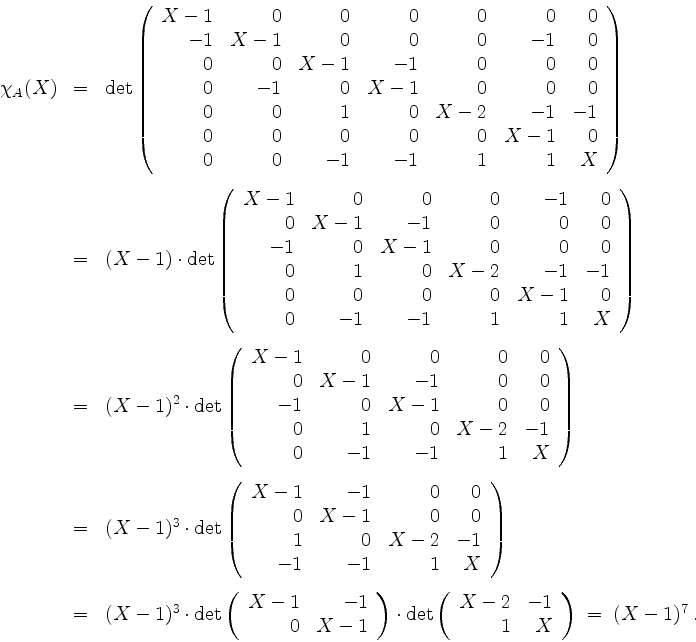
\begin{displaymath} \begin{array}{rcl} \chi_A(X) & = & \det\left( \begin{array}... ...& X \\ \end{array}\right) \; = \; (X - 1)^7\; .\\ \end{array}\end{displaymath}

Wir haben also $ 1$ als einzigen Eigenwert, und dieser hat die algebraische Vielfachheit $ 7$ .

Sei

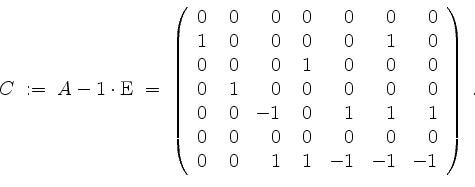
\begin{displaymath} C \; :=\; A - 1\cdot\mathrm{E} \; = \; \left( \begin{array}... ... 0 \\ 0 & 0 & 1 & 1 &-1 &-1 & -1 \\ \end{array}\right) \; . \end{displaymath}

Es wird

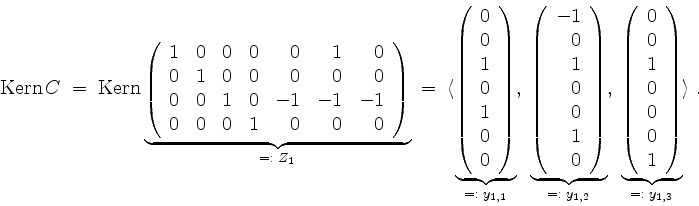
\begin{displaymath} \operatorname{Kern }C \; = \; \operatorname{Kern} \underbrac... ...\\ 0\\ 1\\ \end{array}\right)}_{=:\; y_{1,3}} \rangle\; . \end{displaymath}

Es wird

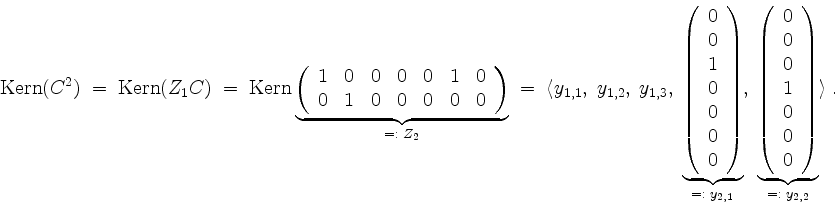
\begin{displaymath} \operatorname{Kern}(C^2)\; =\; \operatorname{Kern}(Z_1 C) \... ...\\ 0\\ 0\\ \end{array}\right)}_{=:\; y_{2,2}} \rangle\; . \end{displaymath}

Es wird

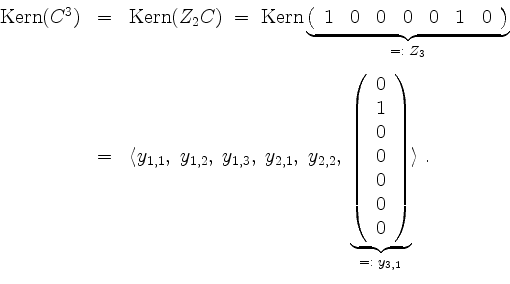
\begin{displaymath} \begin{array}{rcl} \operatorname{Kern}(C^3) &=& \operatornam... ...0\\ \end{array}\right)}_{=:\; y_{3,1}} \rangle\; . \end{array}\end{displaymath}

Es wird

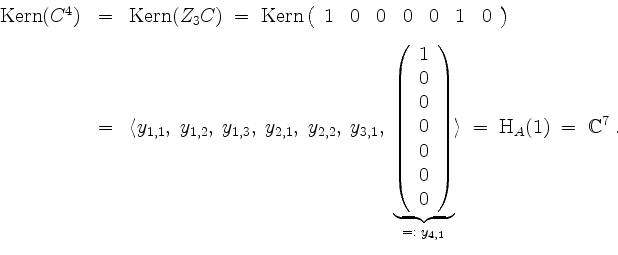
\begin{displaymath} \begin{array}{rcl} \operatorname{Kern}(C^4) &=& \operatornam... ...rangle\; =\; \mathrm{H}_A(1)\; =\; \mathbb{C}^7\; . \end{array}\end{displaymath}

Sei $ x_{4,1} := y_{4,1}$ .

Es ist (zufällig) $ C x_{4,1} = y_{3,1}$ . Es sind keine Vektoren aus $ (y_{3,1})$ auszuwählen, es ist $ (y_{1,1},y_{1,2},y_{1,3},y_{2,1},y_{2,2},C x_{4,1})$ bereits eine Basis von $ \operatorname{Kern}(C^3)$ .

Es ist (zufällig) $ C^2 x_{4,1} = y_{2,2}$ . Wir können den Vektor $ x_{2,1} := y_{2,1}$ aus $ (y_{2,1},y_{2,2})$ auswählen, um eine Basis $ (y_{1,1},y_{1,2},y_{1,3},C^2 x_{4,1}, x_{2,1})$ von $ \operatorname{Kern}(C^2)$ zu erhalten.

Es werden

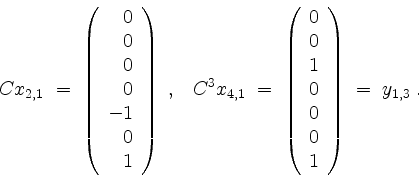
\begin{displaymath} C x_{2,1} \; =\; \left( \begin{array}{r} 0\\ 0\\ 0\\ ... ... 0\\ 0\\ 0\\ 1\\ \end{array}\right) \; =\; y_{1,3} \; . \end{displaymath}

Wir können den Vektor $ x_{1,1} := y_{1,2}$ aus $ (y_{1,1},y_{1,2},y_{1,3})$ auswählen, um eine Basis $ (C^3 x_{4,1},C x_{2,1}, x_{1,1})$ von $ \operatorname{Kern}(C^1)$ zu erhalten.

Insgesamt bilden die Tupel $ \mathrm{Kette}(x_{4,1})$ , $ \mathrm{Kette}(x_{2,1})$ und $ \mathrm{Kette}(x_{1,1})$ eine Basis

$\displaystyle (C^3 x_{4,1},\; C^2 x_{4,1},\; C x_{4,1},\; x_{4,1},\; C x_{2,1},\; x_{2,1},\; x_{1,1} ) $

von $ \mathrm{H}_A(1)$ , deren Vektoren wir in eine Matrix

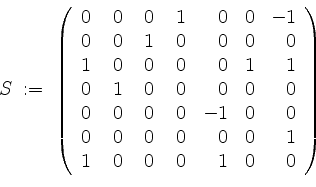
\begin{displaymath} S \; :=\; \left( \begin{array}{rrrrrrr} 0 &\; 0 &\; 0 &\; 1... ...& 0 & 1 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ \end{array}\right) \end{displaymath}

eintragen können. Dann ist

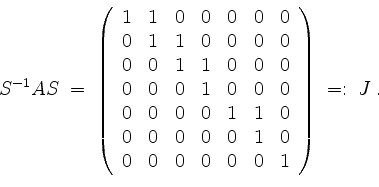
\begin{displaymath} S^{-1} A S \; =\; \left( \begin{array}{rrrrrrr} 1 & 1 & 0 ... ... & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array}\right) \; =: \; J\; . \end{displaymath}

Insbesondere ist

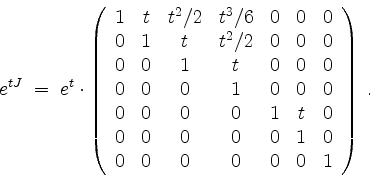
\begin{displaymath} e^{tJ} \; =\; e^t\cdot \left( \begin{array}{ccccccc} 1 & t ... ...& 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array}\right) \; . \end{displaymath}

Somit erhalten wir als allgemeine Lösung der homogenen Gleichung $ u'(t) = A u(t)$ den Funktionenvektor

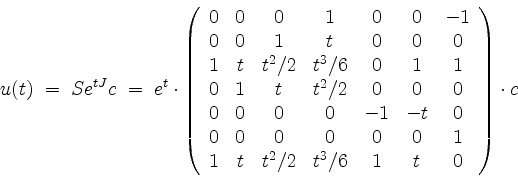
\begin{displaymath} u(t) \; =\; S e^{tJ} c \; =\; e^t\cdot \left( \begin{array}... ... & t & t^2/2 & t^3/6 & 1 & t & 0 \\ \end{array}\right)\cdot c \end{displaymath}

für $ c\in\mathbb{C}^7$ beliebig.

In der partikuläre Lösung taucht der Ausdruck $ S^{-1} b$ auf. Es ist nicht erforderlich, die Inverse $ S^{-1}$ komplett zu berechnen, es ist einfacher, $ S^{-1} b$ als Lösung von $ S(S^{-1}b) = b$ zu bestimmen. (Dies ist immer dann ratsam, wenn der Vektor $ b$ ein Vielfaches eines konstanten Vektors ist.) Wir erhalten

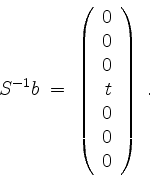
\begin{displaymath} S^{-1} b \; =\; \left( \begin{array}{r} 0\\ 0\\ 0\\ t\\ 0\\ 0\\ 0\\ \end{array}\right)\; . \end{displaymath}

Als partikuläre Lösung der inhomogenen Gleichung $ u'(t) = A u(t) + b$ ergibt sich der Funktionenvektor

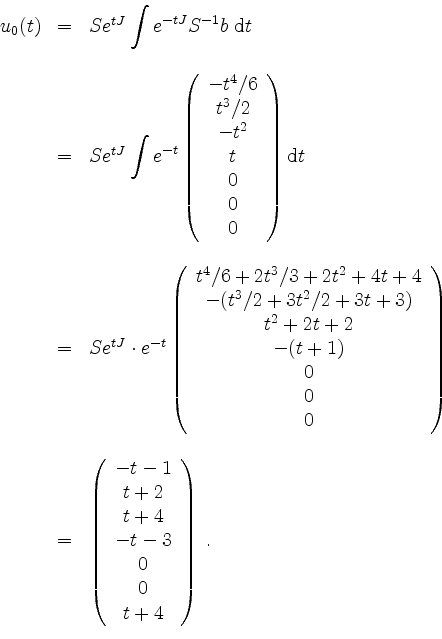
\begin{displaymath} \begin{array}{rcl} u_0(t) & = & S e^{tJ}\displaystyle\int e... ...- 3\\ 0\\ 0\\ t + 4\\ \end{array}\right)\; . \end{array}\end{displaymath}

Die allgemeine Lösung der inhomogenen Gleichung $ u'(t) = A u(t) + b(t)$ setzt sich dann zusammen zu

$\displaystyle u(t) \; =\; u_0(t) + S e^{tJ} c $

für $ c\in\mathbb{C}^7$ beliebig.
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 22.  8. 2006