Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1370: Funktionen_einer_Variablen. Integration. Uneigentliche Integrale.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Untersuchen Sie, ob die folgenden uneigentlichen Integrale existieren, und berechnen Sie gegebenenfalls ihre Werte:

$\displaystyle \begin{array}{ll} {\bf {a)}} \quad {\displaystyle{\int_0^\infty x... ...ty\,\,\frac{dx}{x^2-3x+2}}} \hspace*{0.5cm} & {} \hspace*{4.4cm} \end{array} $


a)

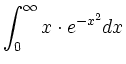
$\displaystyle \int_{0}^{\infty}x\cdot e^{-x^2}dx$

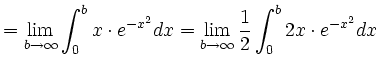
$\displaystyle =\lim_{b\to \infty}\int_{0}^{b}x\cdot e^{-x^2}dx = \lim_{b\to \infty}\frac{1}{2} \int_{0}^{b}2x\cdot e^{-x^2}dx$

Substitution:

$ x^2=u ;\quad \frac{du}{dx}=2x ;\quad du=2x~dx$

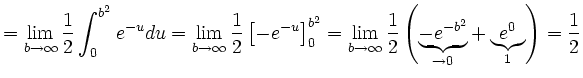
$\displaystyle =\lim_{b\to \infty}\frac{1}{2}\int_{0}^{b^2}e^{-u}du=\lim_{b\to \... ...\left(\underbrace{-e^{-b^2}}_{\to 0}+ \underbrace{e^0}_{1}\right)= \frac{1}{2} $

$ \Longrightarrow$     Integral ist konvergent

b)

$\displaystyle f(x)=\frac{e^{x}}{x}$   auf$\displaystyle \ \ [0,1]$

Existiert$\displaystyle \quad \int_{0}^{1} \frac{e^{x}}{x}~dx= \lim_{a \to\ 0+0}\int_{a}^{1}\frac{e^{x}}{x}~dx\ ?$

Achtung:

zu $ \frac{e^{x}}{x}$ kann keine Stammfunktion in geschlossener Form angegeben werden!

$ e^{x}$ hat die Potenzreihendarstellung:

$\displaystyle e^{x}=1+x+ \underbrace{\frac{x^2}{2!} + \frac{x^3}{3!}+\ldots}_{> 0} > 1+x\quad\Rightarrow \frac{e^{x}}{x}> \frac{1+x}{x}=\frac{1}{x}+1$

Das Integral$\displaystyle \quad \int_{0}^{1} (\frac{1}{x}+1)dx=\underbrace{\int_{0}^{1} \frac{1}{x}dx+1}_{\text{divergent}} \quad \text{existiert nicht!}$

Nach dem Minorantenkriterium ist auch$\displaystyle \quad \int_{0}^{1} \frac{e^x}{x}dx$   divergent$\displaystyle .$

c)

$\displaystyle f(x)=\frac{1}{x^2-3x+2}=\frac{1}{(x-1)(x-2)}=\frac{1}{x-2}-\frac{1}{x-1}$

Es ist:

$\displaystyle \int\frac{1}{x^2-3x+2}~dx\ \ = \frac{1}{x-2}~dx\ \ - \ \frac{1}{x... ... \ln\vert x-2\vert - \ln\vert x-1\vert=\ln \left\vert\frac{x-2}{x-1}\right\vert$

Achtung: $ \displaystyle{\int_{-\infty}^{\infty} f(x)~dx}$ existiert nur, wenn $ \displaystyle{\int_{a}^{b} f(x)~dx}$ für alle Teilintervalle $ [a,b]$ existiert!

Auf [0,1] gilt:

$\displaystyle \int_{-\infty}^{0}\frac{1}{x^2-3x+2}~dx =\lim_{a\to -\infty}\left[\ln\left\vert\frac{x-2}{x-1}\right\vert\right]_{a}^{0}$

$\displaystyle =\lim_{a\to -\infty}\left(\ln 2-\underbrace{\ln\underbrace{\left\... ...{\to 1}}_{\to 0}\right)= \ln 2 \qquad \Longrightarrow \text{Integral existiert}$

Auf [0,1] gilt:

$\displaystyle \int_{0}^{1} \frac{1}{x^2-3x+2}~dx =\lim_{b\to 1-0}\left[\ln\left\vert\frac{x-2}{x-1}\right\vert\right]_{0}^{b}$

$\displaystyle =\lim_{b\to 1-0 }\left (\ln \left \vert\frac{b-2}{b-1}\right\vert- \ln2 \right) = +\infty \qquad \Longrightarrow$   Integral existiert nicht$\displaystyle .$

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[Zurück zur Aufgabe]
  automatisch erstellt am 29. 10. 2006