
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1395: Optimierung eines Zylinders |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Die Oberfläche soll minimert werden, also ist das globale Minimum der Funktion
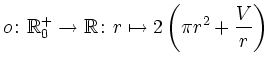
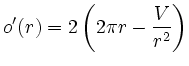 und
und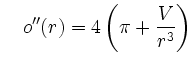 .
.
![$ r_0=\sqrt[3]{\frac{V}{2\pi}}$](/inhalt/loesung/loesung791/img17.png) die einzige
Nullstelle von
die einzige
Nullstelle von ![$ h_0=\frac{V^3\sqrt[3]{2\pi}}{\pi\sqrt[3]{V}}$](/inhalt/loesung/loesung791/img20.png) .
.
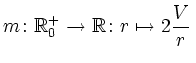 .
.
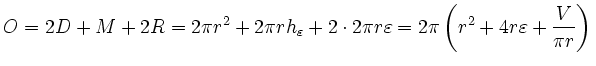 .
.
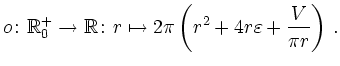
Bei der Untersuchung der Mantelfläche spielt es zunächst, was das qualitative Verhalten der Lösung angeht, keine Rolle, ob man den hinzukommenden Rand mit zur Mantelfläche rechnet oder nicht. Lediglich die Zahlenwerte verändern sich. Die folgende Betrachtung untersucht nur die ,,äußere`` Mantelfäche (entsprechend zum Beispiel einem aufzuklebenden Etikett). Demnach ist die Mantelfläche
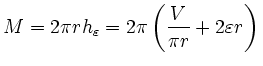 .
.
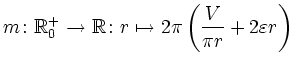
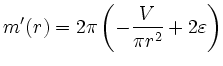 und
und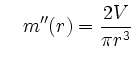 .
.
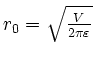 . Diese Nullstelle ist ein lokales Minimum
von
. Diese Nullstelle ist ein lokales Minimum
von | automatisch erstellt am 25. 8. 2006 |