Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1401: Integralberechnung durch partielle Integration

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
a)
Zeigen Sie mit partieller Integration

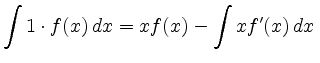$\displaystyle \int 1\cdot f(x)\, d x= xf(x) -\int xf'(x)\, d x\,$.

b)
Berechnen Sie damit die unbestimmten Integrale

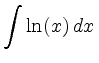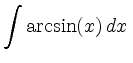$\displaystyle \int\ln(x)\, d x\,$,   $\displaystyle \int\arctan(x)\, d x\,$,   $\displaystyle \int\arcsin(x)\, d x\,$.    

a)
Mit partieller Integration für den Ansatz $ u'(x)=1$ und $ v(x)=f(x)$ folgt $ u(x)=x$ und $ v'(x)=f'(x)$ und man erhält:

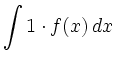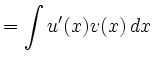$\displaystyle \int 1\cdot f(x)\, d x$ $\displaystyle = \int u'(x)v(x)\, d x$    
  $\displaystyle =\big[u(x)v(x)\big]-\int u(x)v'(x)\, d x$    
  $\displaystyle =\big[xf(x)\big]-\int xf'(x)\, d x\,$.    

b)
Mit obiger Formel erhält man

$\displaystyle \int\ln(x)\, d x =\big[x\ln(x)\big]-\int x\frac{1}{x}\, d x=\big[x\ln(x)-x\big]\,$.    

Weiter gilt:

$\displaystyle \int\arctan(x)\, d x$ $\displaystyle =\big[x\arctan(x)\big]-\frac{1}{2}\int \frac{2x}{1+x^2}\, d x$    
  $\displaystyle =\left[x\arctan(x)-\frac{1}{2}\ln(1+x^2)\right]\,$,    

da der letzte Integrand von der Form $ f'(x)/f(x)$ ist.

Schließlich ist mit Aufgabe 1434:

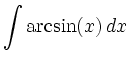$\displaystyle \int\arcsin(x)\, d x$ $\displaystyle =\big[x\arcsin(x)\big]+\frac{1}{2}\int \frac{-2x}{\sqrt{1-x^2}}\, d x$    
  $\displaystyle =\left[x\arcsin(x)+\sqrt{1-x^2}\right]$.    

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 28.  8. 2006