Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1402: Integralberechnung durch partielle Integration

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
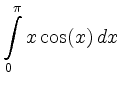Berechnen Sie mit partieller Integration die folgenden Integrale.
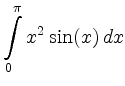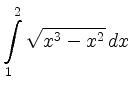
a) $ \displaystyle\int\limits_0^{\pi}x\cos(x)\, d x$                  b) $ \displaystyle\int\limits_0^{\pi}x^2\sin(x)\, d x$                  c) $ \displaystyle\int\limits_1^2\sqrt{x^3-x^2}\, d x$

a)
Mit partieller Integration für den Ansatz $ f'(x)=\cos(x)$ und $ g(x)=x$ erhält man $ f(x)=\sin(x)$ und $ g'(x)=1$ und somit ist:

$\displaystyle \int\limits_0^{\pi}x\cos(x)\, d x =\big[x\sin(x)\big]_{x=0}^{\pi}-\int\limits_0^{\pi}\sin(x)\, d x =0+\big[\cos(x)\big]_{x=0}^{\pi}=-2\,$.

b)
Mit partieller Integration für den Ansatz $ f'(x)=\sin(x)$ und $ g(x)=x^2$ erhält man $ f(x)=-\cos(x)$ und $ g'(x)=2x$ und somit ist:

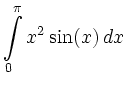$\displaystyle \int\limits_0^{\pi}x^2\sin(x)\, d x$ $\displaystyle =\big[-x^2\cos(x)\big]_{x=0}^{\pi}+2\int\limits_0^{\pi}x\cos(x)\, d x=\pi^2-4$    

unter Verwendung des obigen Ergebnises.
c)
Mit partieller Integration für den Ansatz $ f'(x)=\sqrt{x-1}$ und $ g(x)=x$ erhält man $ f(x)=\frac{2}{3}(x-1)^{3/2}$ und $ g'(x)=1$ und somit ist:

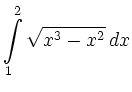$\displaystyle \int\limits_1^2\sqrt{x^3-x^2}\, d x$ $\displaystyle =\int\limits_1^2x\sqrt{x-1}\, d x =\left[x\,\frac{2}{3}(x-1)^{3/2}\right]_{x=1}^2 -\frac{2}{3}\int\limits_1^2(x-1)^{3/2}\, d x$    
  $\displaystyle =\frac{4}{3}-\frac{2}{3}\left[\frac{2}{5}(x-1)^{5/2}\right]_{x=1}^2 =\frac{16}{15}\,$.    

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 25.  8. 2006