Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 1404: Extremwertaufgabe bei Funktionenscharen

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 1404: Extremwertaufgabe bei Funktionenscharen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Gegeben sind die Funktionen $f\colon[0,2]\rightarrow\mathbb{R}\colon x\mapsto -x^2+2x$ und $g_\alpha\colon [0,2]\rightarrow\mathbb{R}\colon x\mapsto 2x+\alpha$ für $\alpha\in\mathbb{R}$ .

a)

Bestimmen Sie das Intervall $I\subseteq\mathbb{R}$ so, dass für alle $\alpha\in I$ die Graphen von

und $g_\alpha$ mindestens einen Schnittpunkt haben, das heißt, dass für alle $\alpha\in I$ gilt:

$\displaystyle \left\{\smash{x\in[0,2]}\left\vert% \vphantom{\smash{x\in[0,2]}}\... ...mash{f(x)=g_\alpha(x)}}\right.\,\smash{f(x)=g_\alpha(x)}\right\} \neq \emptyset$ .

Geben Sie für alle $\alpha\in I$ die Menge $\left\{\smash{x\in[0,2]}\left\vert% \vphantom{\smash{x\in[0,2]}}\vphantom{\smash{f(x)=g_\alpha(x)}}\right.\,\smash{f(x)=g_\alpha(x)}\right\}$ explizit an.

b)

Die Graphen von

und $g_\alpha$ für $\alpha\in I$ schließen die Fläche $F_\alpha$ ein. Bestimmen Sie die Fläche $F_\alpha$ .

c)

Für welche $\alpha\in I$ wird die Fläche $F_\alpha$ maximal, für welche minimal?

a)

Zu untersuchen ist, für welche $\alpha\in\mathbb{R}$ die Lösung

der Gleichung $f(x)=g_\alpha(x)$ im Intervall

liegt. Es gilt:

$\displaystyle f(x)=g_\alpha(x)\iff -x^2+2x=2x+\alpha\iff x^2=-\alpha\,$ .

Dies ist für alle $\alpha\in\mathbb{R}^-_0$ lösbar, nämlich durch $x=\sqrt{-\alpha}$ oder $x=-\sqrt{-\alpha}$ . Letzteres braucht nicht weiter verfolgt zu werden, da nur Lösungen $x\in[0,2]$ interessant sind. Für $\alpha\in[-4,0]$ folgt dann $x\in[0,2]$ . Daher gilt für festes $\alpha\in[-4,0]$ :

$\displaystyle \left\{\smash{x\in[0,2]}\left\vert% \vphantom{\smash{x\in[0,2]}}\... ...x)=g_\alpha(x)}}\right.\,\smash{f(x)=g_\alpha(x)}\right\} =\{\sqrt{-\alpha}\}\,$ .

b)

Die Fläche $F_\alpha$ ist gegeben durch:

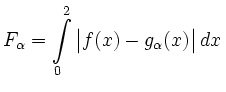$\displaystyle F_\alpha=\int\limits^2_0\big\vert f(x)-g_\alpha(x)\big\vert\, d x\,$ .

Um $F_\alpha$ berechnen zu können ist es nötig zu untersuchen, für welche $x\in[0,2]$ die Ungleichung $f(x)-g_\alpha(x)\leq 0$ erfüllt ist und für welche $x\in[0,2]$ gilt $f(x)-g_\alpha(x)\geq 0$ . Die Funktion $f-g_\alpha$ ist als Differenz stetiger Funktionen stetig, also befinden sich diese Vorzeichenwechsel nur an Nullstellen von $f-g_\alpha$ . Unter (a) wurde gezeigt, dass für $\alpha\in[-4,0]$ gilt:

$\displaystyle \left\{\smash{x\in[0,2]}\left\vert% \vphantom{\smash{x\in[0,2]}}\... ...x)=g_\alpha(x)}}\right.\,\smash{f(x)=g_\alpha(x)}\right\} =\{\sqrt{-\alpha}\}\,$ .

Für $x\in\left[0,\sqrt{-\alpha}\right]$ ist $f(x)-g_\alpha(x)\geq 0$ und für $x\in\left[\sqrt{-\alpha},2\right]$ ist $f(x)-g_\alpha(x)\leq 0$ . Damit ergibt sich:

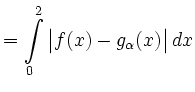$\displaystyle F_\alpha$	$\displaystyle =\int\limits^2_0\big\vert f(x)-g_\alpha(x)\big\vert\, d x$
	$\displaystyle =\int\limits^{\sqrt{-\alpha}}_0\big\vert f(x)-g_\alpha(x)\big\vert\, d x+\int\limits^2_{\sqrt{-\alpha}}\big\vert f(x)-g_\alpha(x)\big\vert\, d x$
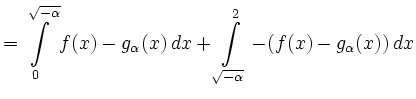	$\displaystyle =\int\limits^{\sqrt{-\alpha}}_0 f(x)-g_\alpha(x)\, d x+\int\limits^2_{\sqrt{-\alpha}} -(f(x)-g_\alpha(x))\, d x$
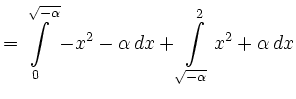	$\displaystyle =\int\limits^{\sqrt{-\alpha}}_0 -x^2-\alpha\, d x+\int\limits^2_{\sqrt{-\alpha}} x^2+\alpha\, d x$
	$\displaystyle =\left[-\frac{1}{3}x^3-\alpha x\right]^{\sqrt{-\alpha}}_0 + \left[\frac{1}{3}x^3+\alpha x\right]^2_{\sqrt{-\alpha}}$
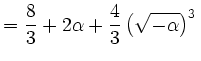	$\displaystyle =\frac{8}{3}+2\alpha+\frac{4}{3}\left(\sqrt{-\alpha}\right)^3\,$ .

c)

Es sind die Parameter $\alpha$ gesucht, für die die zugehörige Fläche $F_\alpha$ maximal beziehungsweise minimal wird. Es ist also die Funktion $F\colon[-4,0]\rightarrow\mathbb{R}\colon \alpha\mapsto F_\alpha$ auf Extremalstellen zu untersuchen. Dazu wird

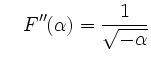
$\displaystyle F'(\alpha)=2-2\sqrt{-\alpha}$ und $\displaystyle \quad F''(\alpha)=\frac{1}{\sqrt{-\alpha}}$

bestimmt.

An der Stelle besitzt demnach einen lokalen Tiefpunkt mit . Da im Inneren des Intervalls keine weiteren lokalen Extrema liegen, befinden sich an den Rändern des Intervalls lokale Hochpunkte, nämlich mit $F(-4)=\frac{16}{3}$ und $F(0)=\frac{8}{3}$ . Die Fläche $F_\alpha$ wird also für $\alpha=-\frac{1}{2}$ minimal und für $\alpha=-4$ maximal.

(Ackermann/Poppitz)

[Zurück zur Aufgabe]

automatisch erstellt am 25. 8. 2006