Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1408: Konvergenzbeweis durch Integralvergleich

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Zeigen Sie mit Hilfe des Integralkriteriums, dass die folgende Reihe für alle $ \alpha\in\mathbb{R}$ mit $ \alpha<-1$ konvergiert (vgl. Aufgabe 1400 c)):

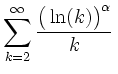$\displaystyle \sum\limits_{k=2}^\infty \frac{\big(\ln(k)\big)^{\alpha}}{k}\,$.

Es sei

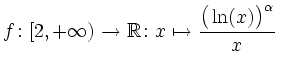$\displaystyle f\colon [2,+\infty)\rightarrow\mathbb{R}\colon x\mapsto\frac{\big(\ln(x)\big)^\alpha}{x}\,$.

Damit ergibt sich

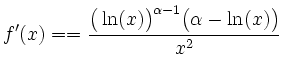$\displaystyle f'(x)= =\frac{\big(\ln(x)\big)^{\alpha-1}\big(\alpha-\ln(x)\big)}{x^2}\,$.

Da $ \alpha<-1$ vorausgesetzt ist, gilt $ f'(x)<0$, das heißt die Funktion $ f$ ist (streng) monoton fallend. Außerdem ist $ f$ positiv. Daher haben nach dem Integralkriterium die Reihe

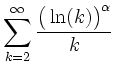
$\displaystyle \sum\limits_{k=2}^\infty \frac{\big(\ln(k)\big)^\alpha}{k} $

und das Integral

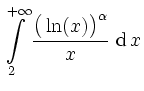
$\displaystyle \int\limits_2^{+\infty} \frac{\big(\ln(x)\big)^\alpha}{x}\,\operatorname{d}x $

das gleiche Konvergenzverhalten. Analog zu Aufgabe 1400 (c) erhält man für $ \alpha<-1$ eine Stammfunktion von $ f$. Damit ergibt sich die Konvergenz des folgenden Integrals:

$\displaystyle \int\limits_2^{+\infty} \frac{\big(\ln(x)\big)^\alpha}{x} =\lim\l... ...alpha+1}}{\alpha+1}\right]_2^t =-\frac{\big(\ln(2)\big)^{\alpha+1}}{\alpha+1}\,$;

folglich konvergiert auch die Reihe

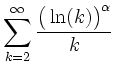$\displaystyle \sum\limits_{k=2}^\infty \frac{\big(\ln(k)\big)^\alpha}{k} $.

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 28.  8. 2006