Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1414: Funktionsuntersuchung einer Funktion zweier Veränderlicher

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Gegeben seien die Funktionen

$\displaystyle g(x,y,z)=z(x^2+y-1)(y^2-1)$   und$\displaystyle \quad \tilde{g}(x,y)=g(x,y,1). $

a)
Geben Sie den Gradienten und die Hesse-Matrix von $ g$ an.
b)
Bestimmen und skizzieren Sie die Mengen

$\displaystyle \widetilde{G}_0:$ $\displaystyle \quad \tilde{g}(x,y)=0$    
$\displaystyle G_0:$ $\displaystyle \quad g(x,y,z)=0$    
$\displaystyle \widetilde{G}_+:$ $\displaystyle \quad \tilde{g}(x,y)>0$    
$\displaystyle \widetilde{G}_-:$ $\displaystyle \quad \tilde{g}(x,y)<0$    

c)
Bestimmen Sie alle kritische Punkte von $ \tilde{g}$ sowie deren Typ.

Zusatz: Bestimmen Sie alle kritischen Punkte von $ g$ und die Mengen:

$\displaystyle G_+:$ $\displaystyle \quad g(x,y,z)>0$    
$\displaystyle G_-:$ $\displaystyle \quad g(x,y,z)<0$    

a)
Es ist

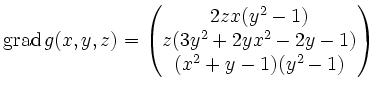
$\displaystyle \operatorname{grad}g(x,y,z)=\left( \begin{matrix} 2zx(y^2-1)\\ z(3y^2+2yx^2-2y-1)\\ (x^2+y-1)(y^2-1) \end{matrix}\right) $

und

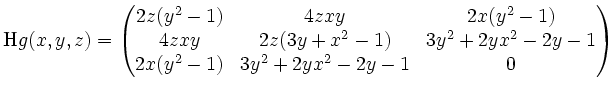
$\displaystyle \mathrm{H}g(x,y,z)=\left( \begin{matrix} 2z(y^2-1) & 4zxy & 2x(y^... ...2-1) & 3y^2+2yx^2-2y-1 \\ 2x(y^2-1) & 3y^2+2yx^2-2y-1 & 0 \end{matrix}\right) $

(durch Ausmultiplizieren kann man die Terme auf eine zum Ableiten angenehmere Form bringen).
b)

Es ist $ 0=\tilde{g}(x,y)=(x^2+y-1)(y^2-1)$ genau dann, wenn $ (x^2+y-1)=0$ oder wenn $ y^2-1=0$ ist. Die erste Gleichung lässt sich umformen in $ y=-x^2+1$, beschreibt also eine ,,nach unten geöffnete`` Parabel mit Scheitelpunkt $ (0,1)$. Die zweite Gleichung ist bereits in der Normalform für Quadriken angegeben und beschreibt ein Paar paralleler ,,horizontaler`` Geraden durch die Punkte $ (0,1)$ und $ (0,-1)$.
\includegraphics[height=.45\linewidth]{H31gebiete}

$\displaystyle \widetilde{G}_0= \left\{{(x,y)\in\mathbb{R}^2}\left\vert\strut \v... ...hantom{\left\vert y\right\vert=1}\right.\, {\left\vert y\right\vert=1}\right\} $

Es ist $ 0=g(x,y,z)=z\,\tilde{g}(x,y)$ genau dann, wenn $ z=0$ oder wenn $ \tilde{g}(x,y)=0$ (und $ z\in\mathbb{R}$ beliebig) ist. Die Gleichung $ z=0$ beschreibt die $ x$-$ y$-Koordinatenebene. Außerdem besteht die Nullstellenmenge aus einer zylindrischen Fläche mit oben beschriebenem Querschnitt.

$\displaystyle G_0= \left\{{(x,y,z)\in\mathbb{R}^3}\left\vert\strut \vphantom{(x... ...m{z=0}\right.\, {z=0}\right\} \cup\left(\widetilde{G}_0\times\mathbb{R}\right) $

\includegraphics[width=.45\linewidth]{H31raeuml2} \includegraphics[width=.45\linewidth]{H31_l_2}

c)
Die Menge $ \widetilde{G}_0$ unterteilt $ \mathbb{R}^2$ in einzelne Gebiete. Da $ p$ stetig ist, reicht es, anhand eines einzelnen Funktionswertes im Inneren des jeweiligen Gebietes zu entscheiden, ob das Gebiet zu $ \widetilde{G}_-$ oder zu $ \widetilde{G}_+$ gehört.

Das ergibt:

$\displaystyle \widetilde{G}_+=\phantom{\cup}$ $\displaystyle \left\{{(x,y)\in\mathbb{R}^2}\left\vert\strut \vphantom{(x,y)\in\mathbb{R}^2}\vphantom{y>1}\right.\, {y>1}\right\}$    
$\displaystyle \cup$ $\displaystyle \left\{{(x,y)\in\mathbb{R}^2}\left\vert\strut \vphantom{(x,y)\in\... ...dge (y<-x^2+1)}\right.\, {(\left\vert y\right\vert<1)\wedge (y<-x^2+1)}\right\}$    
$\displaystyle \cup$ $\displaystyle \left\{{(x,y)\in\mathbb{R}^2}\left\vert\strut \vphantom{(x,y)\in\... ...}^2}\vphantom{(y<-1)\wedge(y>-x^2+1)}\right.\, {(y<-1)\wedge(y>-x^2+1)}\right\}$    

und

$\displaystyle \widetilde{G}_-=\phantom{\cup}$ $\displaystyle \left\{{(x,y)\in\mathbb{R}^2}\left\vert\strut \vphantom{(x,y)\in\... ...dge (y>-x^2+1)}\right.\, {(\left\vert y\right\vert<1)\wedge (y>-x^2+1)}\right\}$    
$\displaystyle \cup$ $\displaystyle \left\{{(x,y)\in\mathbb{R}^2}\left\vert\strut \vphantom{(x,y)\in\... ...}^2}\vphantom{(y<-1)\wedge(y<-x^2+1)}\right.\, {(y<-1)\wedge(y<-x^2+1)}\right\}$    

d)
Es sind die kritischen Punkte zu bestimmen, also die $ (x,y)\in\mathbb{R}^2$, für die $ \operatorname{grad}\tilde{g}(x,y)=0$ gilt. Es ist

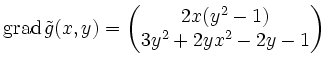$\displaystyle \operatorname{grad}\tilde{g}(x,y)=\left( \begin{matrix} 2x(y^2-1)\\ 3y^2+2yx^2-2y-1 \end{matrix}\right)\,$.

Die Bedingung $ \operatorname{grad}\tilde{g}(x,y)=0$ führt auf die Gleichungen

$\displaystyle 2x(y^2-1)$ $\displaystyle =0$    
$\displaystyle 3y^2+2yx^2-2y-1$ $\displaystyle =0$    

die beide erfüllt sein müssen. Die Gleichung $ 2x(y^2-1)=0$ ist genau dann erfüllt, wenn $ x=0$ oder wenn $ y^2-1=0$.

Der Fall $ x=0$ führt in die Gleichung $ 3y^2+2yx^2-2y-1=0$ eingesetzt auf die Gleichung $ 3y^2-2y-1=0$ und die Lösungen $ y=-\frac{1}{3}$ oder $ y=1$. Dieser Fall liefert also die kritischen Punkte $ P_0=(0,-\frac{1}{3})$ und $ P_1=(0,1)$.

Die Gleichung $ y^2-1=0$ führt auf die Lösungen $ y=1$ oder $ y=-1$. Setzt man $ y=1$ in die Gleichung $ 3y^2+2yx^2-2y-1=0$ ein, so erhält man die Lösung $ x=0$ und damit den bereits ermittelten kritischen Punkt $ P_1$. Setzt man $ y=-1$ in die Gleichung $ 3y^2+2yx^2-2y-1=0$ ein, so erhält man die Lösungen $ x=\sqrt{2}$ oder $ x=-\sqrt{2}$ und damit die kritischen Punkte $ P_2=(\sqrt{2},-1)$ und $ P_3=(-\sqrt{2},-1)$.

Die Punkte $ P_1$ bis $ P_3$ sind Nullstellen von $ \tilde{g}$. Anhand der Skizze erkennt man, dass an diese Punkte jeweils Gebiete angrenzen, in denen $ \tilde{g}$ positive sowie negative Werte annimmt: Diese Punkte sind also Sattelpunkte.

Ebenfalls anhand der Skizze erkennt man, dass $ P_0$ der einzige kritische Punkt der stetigen Funktion $ \tilde{g}$ im Inneren des kompakten Gebietes $ \left\{{(x,y)\in\mathbb{R}^2}\left\vert\strut \vphantom{(x,y)\in\mathbb{R}^2}\... ...q-x^2+1)}\right.\, {(\left\vert y\right\vert\leq1)\wedge(y\geq-x^2+1)}\right\} $ ist, dessen Rand aus Nullstellen von $ \tilde{g}$ besteht. Im Inneren des Gebiets nimmt $ \tilde{g}$ ausschließlich positive Werte an. Nach dem Satz vom Minimum und Maximum besitzt $ \tilde{g}$ in dem Gebiet ein Maximum, das aus Mangel an Alternativen an der einzigen kritischen Stelle im Inneren liegen muss. Bei $ P_0$ besitzt $ \tilde{g}$ also einen Hochpunkt.

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 25.  8. 2006