Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1416: Extrema unter Nebenbedingungen mittels Lagrange-Multiplikatoren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Bestimmen Sie mit der Methode von Lagrange die Extrema der Funktion

$\displaystyle f(x,y,z)=x+y-z $

unter der Nebenbedingung

$\displaystyle x^2+y^2+z^2=1\,. $

Um die Lagrange-Multiplikatoren-Methode anwenden zu können, ist zunächst eine geeignete Funktion $ g$, die die Nebenbedingungen beschreibt, zu finden. Dies ist mit

$\displaystyle g\colon\mathbb{R}^3\rightarrow\mathbb{R}\colon (x,y,z)\mapsto x^2+y^2+z^2-1 $

gegeben, denn es gilt $ g(x_0,y_0,z_0)=0$ genau dann, wenn die Gleichung $ x_0^2+y_0^2+z_0^2=1$ erfüllt ist.

Mit der Lagrange-Multiplikatoren-Methode werden nun die kritischen Stellen, an denen Extrema vorliegen können, bestimmt. Die Bedingungen

$\displaystyle g(x,y,z)$ $\displaystyle =0$    
$\displaystyle \operatorname{grad}f(x,y,z)+\lambda\operatorname{grad}g(x,y,z)$ $\displaystyle =0$    

führen auf das folgende Gleichungssystem:

$\displaystyle x^2+y^2+z^2-1$ $\displaystyle =0$ (1)
$\displaystyle 1+2\lambda x$ $\displaystyle =0$ (2)
$\displaystyle 1+2\lambda y$ $\displaystyle =0$ (3)
$\displaystyle -1+2\lambda z$ $\displaystyle =0$ (4)

Der Fall $ \lambda=0$ stünde im Widerspruch zu den Gleichungen $ (2)$, $ (3)$ und $ (4)$. Unter der Annahme $ \lambda\neq 0$ ergibt sich aus diesen Gleichungen:

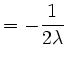$\displaystyle x=y$ $\displaystyle =-\frac{1}{2\lambda}$    
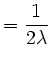$\displaystyle z=-y$ $\displaystyle =\frac{1}{2\lambda}$    

Diese Werte in Gleichung $ (1)$ eingesetzt liefern:

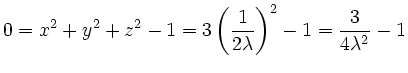
$\displaystyle 0=x^2+y^2+z^2-1=3\left(\frac{1}{2\lambda}\right)^2-1=\frac{3}{4\lambda^2}-1 $

und damit

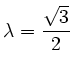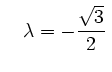$\displaystyle \lambda = \frac{\sqrt{3}}{2}$   oder$\displaystyle \quad \lambda =-\frac{\sqrt{3}}{2}\,$.

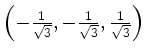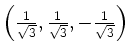Der Fall $ \lambda = \frac{\sqrt{3}}{2}$ führt auf die kritische Stelle $ \left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\right)$, der Fall $ \lambda = -\frac{\sqrt{3}}{2}$ führt auf die kritische Stelle $ \left(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)$. Da die Menge $ \left\{\smash{v\in\mathbb{R}^3}\left\vert% \vphantom{\smash{v\in\mathbb{R}^3}}\vphantom{\smash{g(v)=0}}\right.\,\smash{g(v)=0}\right\} $ kompakt ist, nimmt die Funktion $ f$ dort unter der gegebenen Nebenbedingung nach dem Satz vom Minimum und Maximum auch ein Minimum und ein Maximum an. Dies kann nur an den oben berechneten kritischen Stellen geschehen. Ein Vergleich der Funktionswerte von $ f$ an diesen kritischen Stellen zeigt:

An der Stelle 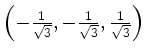$ \left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\right)$ liegt ein Minimum vor, an der Stelle 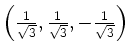$ \left(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)$ liegt ein Maximum vor.

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 25.  8. 2006