Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1460: Lagrange-Multiplikator.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Verwenden Sie den Lagrange-Multiplikator um die Zielfunktion $ f(x,y,z)= xyz$ unter der Nebenbedingung $ x^2+y^2+z^2=4$ zu maximieren, vorausgesetzt $ x,y,z \geq 0$.

Bilde zuerst die Funktion für die Nebenbedingung

$\displaystyle g(x,y,z) = x^2+y^2+z^2-4. $

Dann definiere eine neue Funktion $ F(x,y,z,\lambda)$ durch
$\displaystyle F(x,y,z,\lambda)$ $\displaystyle =$ $\displaystyle f(x,y,z) - \lambda g(x,y,z),$  
  $\displaystyle =$ $\displaystyle xyz - \lambda (x^2+y^2+z^2-4).$  

Um die kritischen Punkte der neuen Funktion $ F(x,y,z,\lambda)$ zu finden, berechne die ersten partiellen Ableitungen von $ F$ nach $ x,y,z,\lambda$ und setze sie gleich 0.

$\displaystyle F_x$ $\displaystyle =$ $\displaystyle yz - \lambda (2x) = 0.$  
$\displaystyle F_y$ $\displaystyle =$ $\displaystyle xz - \lambda (2y) = 0.$  
$\displaystyle F_z$ $\displaystyle =$ $\displaystyle xy - \lambda (2z) = 0.$  
$\displaystyle F_\lambda$ $\displaystyle =$ $\displaystyle x^2+y^2+z^2-4 = 0.$  

Jetzt haben wir $ 4$ Gleichungen mit $ 4$ Unbekannten $ (x,y,z,\lambda)$, welche wir lösen müssen.

Es gibt verschiedene Wege dieses Gleichungssystem zu lösen. Ein Weg ist, die erste durch die zweite Gleichung zu teilen um $ \lambda$ zu eliminieren.

$\displaystyle y/x = x/y \;\;\;$   or$\displaystyle \;\;\; x^2 = y^2. $

Das Gleiche machen wir mit der zweiten und dritten Gleichung

$\displaystyle z/y = y/z \;\;\;$   or$\displaystyle \;\;\; z^2 = y^2. $

Entsprechend können wir die folgende Beziehung zwischen den Variablen $ x,y,z$ herleiten.

$\displaystyle x^2=y^2=z^2. $

Eingesetzt in die vierte Gleichung ergibt

$\displaystyle x^2+x^2+x^2=4 \;\;\; \to \;\;\; x = \sqrt{4/3} = 2/\sqrt{3}. $

Benütze den Wert von $ x$ um durch Rücksubstituieren die andern Variablen zu berechnen. Beachte, dass $ x,y,z \geq 0$.

$\displaystyle x=y=z=2/\sqrt{3}, \;\;\; \lambda = x/2 = 1/\sqrt{3}. $

So kann der maximale Wert der Zielfunktion $ f(x,y,z)$ berechnet werden

$\displaystyle f_{max}(x,y,z) = (2/\sqrt{3})(2/\sqrt{3})(2/\sqrt{3}) = 8/\sqrt{27}. $

Es empfiehlt sich zu überprüfen, ob die erhaltene Lösung die Nebenbedingung erfüllt.

$\displaystyle x^2+y^2+z^2 = 3x^2 = 3(4/3) = 4.$

Hesse:

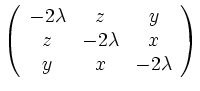
$\displaystyle \left(\begin{array}{ccc} -2\lambda & z & y \\ z & -2\lambda & x \\ y & x & -2\lambda \\ \end{array}\right) $

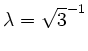In unserem Punkt $ \lambda= \sqrt {3}^{-1}$.

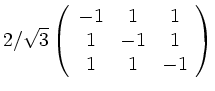
$\displaystyle 2/\sqrt{3} \left(\begin{array}{ccc} -1& 1 & 1 \\ 1 & -1 & 1 \\ 1 & 1 & -1 \\ \end{array}\right) $

Eigenwerte: $ \lambda_{1,2}=-2$, $ \lambda_3=1$.

$ v_3=(1 1 1)^\top=c\nabla g$. Also negativ definit ausserhalb den Vektoren, die auf $ \nabla g$ senkrecht stehen.

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[Zurück zur Aufgabe]
  automatisch erstellt am 17.  9. 2006