Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1466: Jakobi-Matrix.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Sei

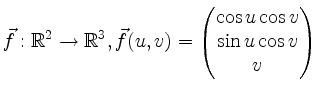
$\displaystyle \vec{f}: {\mathbb{R}}^2\to{\mathbb{R}}^3, \vec{f}(u,v)= \begin{pmatrix} \cos u \cos v \\ \sin u \cos v\\ v \end{pmatrix}$

Berechnen Sie die Jakobi-Matrix $ \nabla\vec{f}$ . Für welche Punkte ist der Rang von $ \nabla\vec{f}$ gleich $ 2$ ?

Bezeichne $ (\nabla\vec{f},\vec{e}_i)$ die $ 3\times 3$ Matrix, deren ersten beiden Spalten aus den Spalten der Jakobi-Matrix besteht, und deren dritte Spalte gleich $ \vec{e}_i$ ist.

Berechnen Sie die Oberfläche der durch $ f$ parametrisierten Fläche

$\displaystyle \int \sqrt{\sum_{i=1}^3 \big(\det (\nabla\vec{f},\vec{e}_i)\big)^2} \,d u \,d v $

für $ 0<u\leq 2\pi$ und $ v$ begrenzt durch die Punkte mit $ \mathrm{rg}\, \nabla\vec{f} = 1$ .

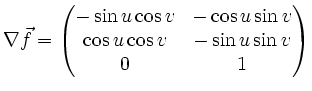
$\displaystyle \nabla\vec{f}=\begin{pmatrix} -\sin u \cos v & -\cos u \sin v\\ \cos u \cos v & - \sin u \sin v \\ 0 & 1 \end{pmatrix}$

Für Rang 2 hinreichend

$\displaystyle \sin^2u\cos v \sin v + \cos^2u \cos v \sin v= \cos v \sin v \neq 0 $

also Rang 1 genau für $ \cos v=0$.

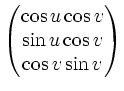
$\displaystyle \begin{pmatrix} \cos u \cos v\\ \sin u \cos v\\ \cos v \sin v \end{pmatrix}$

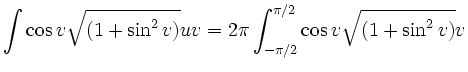
$\displaystyle \int \cos v \sqrt{ (1+\sin^2v)} \di u \di v = 2\pi \int_{-\pi/2}^{\pi/2} \cos v \sqrt{ (1+\sin^2v)} \di v $

Substitution $ z=\sin v, \di z = \cos v \di v$

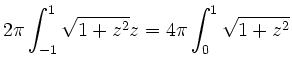
$\displaystyle 2\pi\int_{-1}^{1} \sqrt{1+z^2} \di z=4\pi\int_{0}^{1} \sqrt{1+z^2} $

$ z=\sinh x, \di z = \cosh x \di x $

$\displaystyle 4\pi \int_0^{\mathrm{arcsinh}\,1} \cosh^2 x \di x = \pi \int (e^{... ...2}+2x\right]_0^{\mathrm{arcsinh}\,1}= 2\pi ( \sqrt{2} + \mathrm{arcsinh}\,2 ) $

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[Zurück zur Aufgabe]
  automatisch erstellt am 17.  9. 2006