Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1467: Kettenregel für vektorwertige Funktionen.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
  1. Beweisen Sie die Kettenregel für vektorwertige Funktionen:

    Seien

    $\displaystyle \vec{g}: D\subseteq {\mathbb{R}}^n \to {\mathbb{R}}^m$$\displaystyle \quad \text { und } \quad \vec{f}: g(D) \to {\mathbb{R}}^l $

    stetig differenzierbare vektorwertige Funktionen. Dann ist auch die Komposition

    $\displaystyle \vec{f}\circ \vec{g}: D\subseteq {\mathbb{R}}^n \to {\mathbb{R}}^l $

    stetig differenzierbar und es gilt

    $\displaystyle \nabla(\vec{f}\circ \vec{g})(\vec{x})=\nabla(\vec{f}( \vec{g}(\vec{x})) =(\nabla\vec{f})(\vec{g}(\vec{x})) (\nabla\vec{g})(\vec{x})\,, $

    m.a.W. die Jacobi-Matrix der Komposition $ \vec{f}\circ \vec{g}$ an der Stelle $ \vec{x}$ ist das Matrixprodukt der Jacobi-Matrix von $ \vec{f}$ an der Stelle $ \vec{g}(x)$ und der Jacobi-Matrix von $ \vec{g}$ an der Stelle $ \vec{x}$.

    Hinweis: ein eleganter und kurzer Beweis benutzt direkt die Definition der Jakobi-Matrix

    $\displaystyle \vec{f}(\vec{x}+\vec{h}) = \vec{f}(\vec{x}) + (\nabla\vec{f})(\vec{x})\vec{h} + o(\vec{h}) $

  2. Berechnen Sie mit Hilfe obiger Kettenregel die Jacobi-Matrix der Funktion $ \vec{f}\circ \vec{g}$ mit

    \begin{displaymath} \begin{array}{rrcllrrcl} g:& {\mathbb{R}}^2 &\to&{\mathbb{R}... ...begin{pmatrix} \cos x_1\\ \sin x_2 \end{pmatrix}\end{array}\,. \end{displaymath}

  3. Zeigen Sie: Ist $ f:D\subseteq {\mathbb{R}}^n\to{\mathbb{R}}^m$ total differenzierbar, injektiv und $ f^{-1}:\mathrm{Im}f\subseteq{\mathbb{R}}^m\to{\mathbb{R}}^n$ ebenfalls total differenzierbar, so folgt für alle $ \vec{x}\in D$

    $\displaystyle {\nabla(\vec{f}^{-1})}(\vec{f}(\vec{x})) {\nabla \vec{f}}(\vec{x}) = E_n $

Die Funktionen $ \vec f$ und $ \vec g$ sind total differenzierbar, also gilt
$\displaystyle \vec g(\vec x+ \vec h)$ $\displaystyle =$ $\displaystyle \vec g(\vec x) + \nabla\vec g(\vec x)\vec h + o(\vec h)$  
$\displaystyle \vec f(\vec x+ \vec h)$ $\displaystyle =$ $\displaystyle \vec f(\vec x) + \nabla\vec f(\vec x)\vec h + o(\vec h)$  

und daher mit $ \vec k= \nabla\vec g(\vec x)\vec h + o(\vec h)$
$\displaystyle \vec f\circ \vec g(\vec x+ \vec h)$ $\displaystyle =$ $\displaystyle \vec f(\vec g(\vec x) + \nabla\vec g(\vec x)\vec h + o(\vec h))=\vec f(g(\vec x)+ \vec k)$  
  $\displaystyle =$ $\displaystyle \vec f(\vec g(\vec x)) + \nabla\vec f(\vec g(\vec x)) \vec k + o(\vec k)$  
  $\displaystyle =$ $\displaystyle \vec f(\vec g(\vec x)) + \nabla\vec f(\vec g(\vec x)) \nabla\vec ... ...bla\vec f(\vec g(\vec x)) o(\vec h) + o(\nabla\vec g(\vec x)\vec h + o(\vec h))$  

Da die Einträge der Jabobi-Matrizen stetig differenzierbarer Funktionen beschränkt sind, gilt

$\displaystyle \nabla\vec f(\vec g(\vec x)) o(\vec h) + o(\nabla\vec g(\vec x)\vec h + o(\vec h)) =o(\vec h) $

und somit

$\displaystyle \nabla \vec f\circ \vec g(\vec x) = \nabla\vec f(\vec g(\vec x)) \nabla\vec g(\vec x) $

Im Beispiel ist

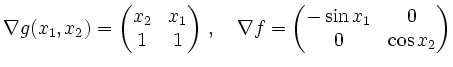
$\displaystyle \nabla g(x_1,x_2) = \begin{pmatrix} x_2 & x_1 \\ 1 &1 \end{pma... ..., \quad \nabla f = \begin{pmatrix} -\sin x_1 & 0 \\ 0& \cos x_2 \end{pmatrix}$

und daher

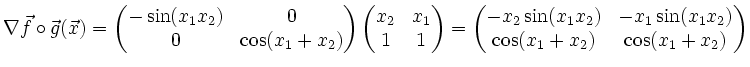
$\displaystyle \nabla \vec f\circ \vec g(\vec x) = \begin{pmatrix} -\sin (x_1x_... ...(x_1x_2) & -x_1\sin (x_1x_2) \\ \cos (x_1+x_2) & \cos (x_1+x_2) \end{pmatrix}$

Zuletzt gilt untern den Voraussetzungen von Teil iii)

$\displaystyle \vec{f}^{-1}(\vec{f}(\vec{x})) = \vec{x} $

mit Kettenregel

$\displaystyle {\nabla(\vec{f}^{-1})}(\vec{f}(\vec{x})) {\nabla \vec{f}}(\vec{x}) = E_n $

da

$\displaystyle \vec{x} = 0 + E_n\vec{x} $

also $ E_n$ die totale Ableitung der identischen Funktion ist.
(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[Zurück zur Aufgabe]
  automatisch erstellt am 17.  9. 2006