Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1473: Normalgebiet und Schwerpunkt.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Sei $ B\subseteq {\mathbb{R}}^3$ ein Normalgebiet mit Volumen $ V=\int \int \int_B\,d x_3\,d x_2 \,d x_1$. Der Schwerpunkt $ (\mo{s}{1},\mo{s}{2},\mo{s}{3})$ von $ B$ (bei homogener Massenverteilung) ist gegeben durch
$\displaystyle \mo{s}{1}$ $\displaystyle =$ $\displaystyle \frac 1V \int\int\int_B x_1 \,d x_3 \,d x_2 \,d x_1\,,$  
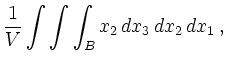$\displaystyle \mo{s}{2}$ $\displaystyle =$ $\displaystyle \frac 1V \int\int\int_B x_2 \,d x_3 \,d x_2 \,d x_1\,,$  
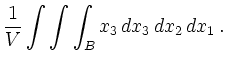$\displaystyle \mo{s}{3}$ $\displaystyle =$ $\displaystyle \frac 1V \int\int\int_B x_3 \,d x_3 \,d x_2 \,d x_1\,.$  

Wir betrachten den durch die Koordinatenebenen $ x_1=0$, $ x_2=0$, $ x_3=0$ sowie durch die Ebenen $ 2x_1+x_2=6$ und $ 6x_1+3x_2+4x_3=24$ begrenzten räumlichen Bereich $ B$. Zeigen Sie, dass $ B$ ein Normalgebiet ist, skizzieren Sie $ B$ und berechnen Sie seinen Schwerpunkt.
Man betrachtet den durch die Koordinatenebenen $ x_1=0$, $ x_2=0$, $ x_3=0$ sowie durch die Ebenen $ 2x_1+x_2=6$ und $ 6x_1+3x_2+4x_3=24$ begrenzten räumlichen Bereich.

Man kann diesen räumlichen Bereich auch beschreiben durch folgende Bedingungen:


0 $\displaystyle \leq x_1$ $\displaystyle \leq 3$  
$\displaystyle 0=f(x_1)$ $\displaystyle \leq x_2$ $\displaystyle \leq (6-2x_1)=g(x_1)$  
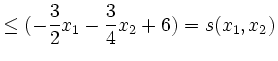$\displaystyle 0=r(x_1,x_2)$ $\displaystyle \leq x_3$ $\displaystyle \leq (-\frac{3}{2}x_1-\frac{3}{4}x_2+6)=s(x_1,x_2)$  

Da der betrachtete räumliche Bereich sich in dieser Weise darstellen lässt, und alle verwendeten Funktionen (mindestens) einmal stetig differenzierbar sind, handelt es sich um ein Normalgebiet.
Um den Schwerpunkt des Normalgebietes zu bestimmen, wird zunächst dessen Volumen berechnet:


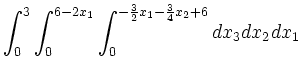$\displaystyle V$ $\displaystyle =$ $\displaystyle \int_0^3 \int_0^{6-2x_1} \int_0^{-\frac{3}{2}x_1-\frac{3}{4}x_2+6} dx_3 dx_2 dx_1$  
  $\displaystyle =$ $\displaystyle \int_0^3 \int_0^{6-2x_1} \left [ x_3 \right ]_0^{-\frac{3}{2}x_1-\frac{3}{4}x_2+6} dx_2 dx_1$  
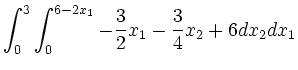  $\displaystyle =$ $\displaystyle \int_0^3 \int_0^{6-2x_1} -\frac{3}{2}x_1-\frac{3}{4}x_2+6 dx_2 dx_1$  
  $\displaystyle =$ $\displaystyle \int_0^3 \left [-\frac{3}{2}x_1x_2-\frac{3}{8}x_2^2+6x_2 \right ]_0^{6-2x_1}$  
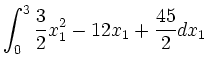  $\displaystyle =$ $\displaystyle \int_0^3 \frac{3}{2}x_1^2-12x_1+\frac{45}{2} dx_1$  
  $\displaystyle =$ $\displaystyle \left [ \frac{1}{2}x_1^3-6x_1^2+\frac{45}{2}x_1 \right ]_0^3 = 27$  

Für die Schwerpunktskoordinaten ergibt sich mit äquivalenter Rechnung zu oben:

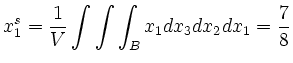
$\displaystyle x_1^s = \frac{1}{V}\int\int\int_B x_1 dx_3 dx_2 dx_1 = \frac{7}{8} $

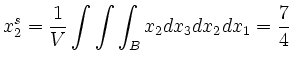
$\displaystyle x_2^s = \frac{1}{V}\int\int\int_B x_2 dx_3 dx_2 dx_1 = \frac{7}{4} $

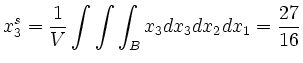
$\displaystyle x_3^s = \frac{1}{V}\int\int\int_B x_3 dx_3 dx_2 dx_1 = \frac{27}{16} $

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[Zurück zur Aufgabe]
  automatisch erstellt am 17.  9. 2006