Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 1483: Allgemeine Lösung einer DGL und Anfangswertproblem.

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 1483: Allgemeine Lösung einer DGL und Anfangswertproblem.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Berechnen Sie die allgemeine Lösung der DGL

$\displaystyle y'' +y = \sin t$
(angeregte Schwingung). Zeichnen Sie den Graphen der Lösung für die Anfangswerte , .
Lösen Sie folgendes Anfangswertproblem

$\displaystyle y'' -2y' +y=0\,, \quad y(0)=1, y'(0)=2\,.$

Man betrachtet die Differentialgleichung einer angeregten Schwingung:

$\displaystyle y''+y=\sin t$

Zu ihrer Lösung bestimmt man zunächst die allgemeine Lösung der zugehörigen homogenen Differentialgleichung . Die charakteristische Gleichung dieser DGL lautet:

$\displaystyle \lambda^2+1=0$

Deren Nullstellen sind:

$\lambda_{1}= i$ , $\lambda_{2}= -i$

Im Falle zweier konjugiert komplexer Nullstellen $\lambda_{1/2}=\alpha \pm i \beta$ wählt man folgende Lösungsbasis:

$y_1(t)= e^{\alpha t}\cos \beta t$ , $y_2(t)= e^{\alpha t}\sin \beta t$

Man erhält hier also für die vollständige allgemeine Lösung der homogenen DGL:

$\displaystyle y_h(t) = c_1\cos t+ c_2\sin t$

Für die partikuläre Lösung setzen wir

$\displaystyle y_p(t) = c_1(t)\cos t + c_2(t)\sin t$
und bekommen durch einsetzen in die DGL

$\displaystyle c_1''\cos t - 2c_1' \sin t - c_1 \cos t + c_2''\sin t + 2c_2'\cos t -c_2\sin t + c_1\cos t + c_2 \sin t = \sin t$
Durch Koeffizientenvergleich erhalten wir das DGL System

$\displaystyle c_1'' + 2c_2'$ $\displaystyle =$ 0

$\displaystyle -2c_1' +c_2''$ $\displaystyle =$ $\displaystyle 1$

Aus der ersten Gleichung sieht man durch integrieren, dass und somit müssen wir die DGL

$\displaystyle c_2'' +4 c_2=1$
lösen. Wir erraten die Lösung und berechnen . Eine spezielle Lösung ist also

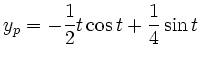
$\displaystyle y_p= - \frac 12 t \cos t + \frac 14 \sin t$

Eine Alternative ist, die DGL 2. Ordnung auf ein System erster Ordnung umzuschreiben und dann in gewohnter Weise zu lösen.
Damit ergibt sich als allgemeine Lösung der vorliegenden DGL:

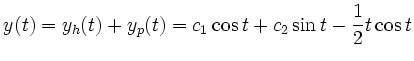
$\displaystyle y(t) = y_h(t) + y_p(t) = c_1\cos t+ c_2\sin t -\frac{1}{2}t\cos t$
Man betrachtet die Differentialgleichung

$\displaystyle y''-2y'+y=0$

Die charakteristische Gleichung dieser DGL lautet:

$\displaystyle \lambda^2-2\lambda+1=0$

Diese besitzt nur eine doppelte Nullstelle:

$\lambda= 1$

Im Falle einer doppelten, reellen Nullstelle erhält man lediglich folgende Basislösung:

$\displaystyle y_1(x) = e^x$

Mit Variation der Konstanten, also ergibt sich als allgemeine Lösung:

$\displaystyle y(x) = (c_1x+c_2)e^x$

mit den linear unabhängigen, reellen Basislösungen:

,

Mit den Anfangswerten

,

ergibt sich als Lösung der homogenen DGL 2. Ordnung:

$\displaystyle y(x) = (x+1)e^x$